为不失一般性，下面研究相对平衡流体的平衡微分方程。

如图2．4所示，在相对平衡流体中任取一个边长为δx、δy及δz的微小六面体。该六面体受表面力及质量力的作用而处于平衡状态。设六面体中心点A（x，y，z）的压强为p，因为压强在平衡流体中是空间坐标的连续函数，即p＝p（x，y，z），按照多元连续函数的泰勒级数展开式，略去二阶以上的微量后，便得到微小六面体各侧面上的压强，从而可计算得各侧面的表面力。

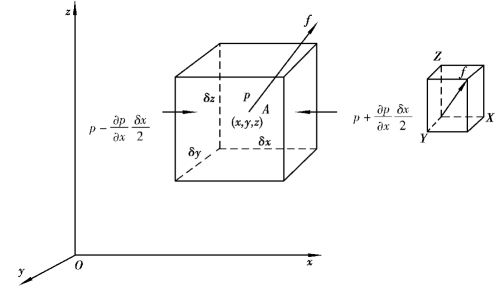
图2．4　平衡微小六面体

以与x轴正交的左右两个侧面为例：

左侧面

右侧面

则x向的表面力合力为

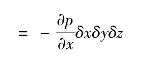
同理可得出y、z向的表面力的合力，即

除了表面力外，该微小六面体还受质量力的作用。设单位质量力f为空间任意方向，它在各轴向的分量为X、Y、Z，故x向的质量力为Xρδxδyδz，y向为Yρδxδyδz，z向为Zρδxδyδz。

由此可得各轴向的合力分别为

x向

y向

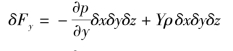
z向

作用在该微小六面体上的合力矢量用下式表示，即

用该微元体的体积δxδyδz＝δv除上式后，便得到精确的表达式，即(www.daowen.com)

这就是一点上单位体积合力的表达式。对于平衡流体，此合力必定等于零，即

式中，第一项括号内的量是梯度，第二括号内是单位质量力f＝Xi＋Yj＋Zk，则式（2．2）可写为

式（2．3）是流体静力学的基本公式，它表明压强的最大变化率发生在质量力矢量的方向上。

式（2．3）也可写成分量的形式，即

此式为流体平衡微分方程式。它是由欧拉在1755年首先导出，故又称为欧拉平衡方程式。它说明在平衡流体中作用于单位体积上同一轴向的质量力分量（ρX、ρY、ρZ）与表面力分量相等。表明压强沿某轴向的变化率等于该轴向单位体积上的质量力分量。因此，如果平衡流体中某方向无质量力的分量，则该方向就没有压强的变化。

式（2．4）还可以写成另一种表达式，将各式依次乘以dx、dy、dz，然后相加经移项得

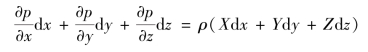
因为p＝p（x，y，z），所以上式等号左边为静压强p的全微分dp，则平衡方程又可表示为

dp＝ρ（Xdx＋Ydy＋Zdz）　（2．5）

流体密度ρ是个常数，因而从数学角度来分析，式（2．5）右边括号内三项总和必然是某一函数W（x，y，z）的全微分，即

dW＝Xdx＋Ydy＋Zdz　（2．6）

而

由此得

满足式（2．7）的函数W（x，y，z）称为力函数（势函数），具有这样力函数的质量力称为有势力。由此可得到结论：流体只有在有势的质量力的作用下才能保持平衡。

将质量力用势函数表示，则平衡方程又可表示为

dp＝ρdW　（2．8）

积分得p＝ρW＋C，C为积分常数。若已知液体内部或表面某点处的力函数W0和压强p0，则有

p＝p0＋ρ（W－W0）　（2．9）

这就是不可压缩流体平衡微分方程积分后静止流体内任一点压强p的普遍表达式。