根据流体定义，静止流体内不存在切应力，因而表面力只有垂直于作用面的压力。作用于流体单位面积上的压力称为压强。在平衡的流体微团表面取一微元面ΔA，设作用在ΔA上的压力为ΔP，则称为ΔA面上的平均压强，当ΔA缩小为一点时，有

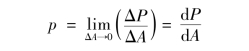
称为点上的流体静压强。流体静压强有两个重要特性：一是流体静压强的方向与作用面的方位有关，它始终沿着作用面的内法线方向，读者可自行加以证明；二是压强的大小与作用面的方位无关，静止流体内任一点上的压强沿各方向相等。为了证明这一性质，在绝对静止流体内的任一点（x，y）取出一单位宽度的微小楔形分离体，如图2．3所示，因为该分离体没有切力的作用，只有重力和垂直于各表面上的压力，所以沿x和z向的平衡方程为

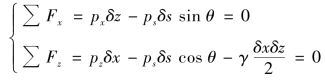
式中，px、pz及ps分别是三个面上的平均压强，γ是流体的重度，ρ是密度。

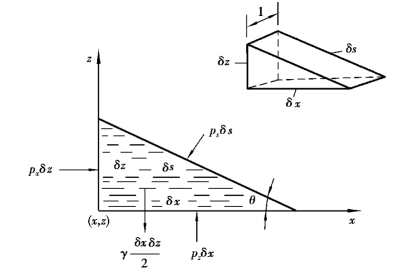
图2．3　静压强特性

根据几何关系：

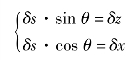(www.daowen.com)

上述方程组简化为

忽略高阶无穷小量可得

px＝pz＝ps

因为θ是任意角，所以上式就证明了在静止流体内任一点上的静压强各方向相同。对于由三个坐标面和一个任意斜面构成的微小四面体的三维情况，利用平衡方程，同样可证明。

px＝py＝pz＝ps

不难证明，对于还有其他惯性力作用的相对静止流体内，也可得到同样的结果。

虽然同一点上的静压强沿各方向相等，但是不同的点一般说来其大小不同。由于流体可看作连续介质，所以流体静压强应是空间坐标的连续函数，即

p＝p（x，y，z）　（2．1）