流体的黏温特性对于工程设计和生产管理来说，是必须要考虑的重要问题。由流体黏滞性的产生原因可知：对于液体，当温度升高时，分子之间的内聚力将减小，其黏性就减小；对于气体，当温度升高时，分子活动加剧，分子碰撞的机会增多，动量交换增大，其黏性反而相应加大。

1）黏温特性的一般模型方程

对于牛顿流体（如图1．2所示），黏温特性的一般数学模型方程常用以下三种：

①塔曼—汉斯公式

式中，a、b、c为通过曲线方程模拟而得到的三个参数（见表1．5）；t为流体的实际温度，℃。上式也称为三参数指数关系式。

②重对数计算式

式中，a、b、c同上，为三个参数；T为流体的实际温度，K。(www.daowen.com)

上面两式中，ν为实际运动黏度，一般单位为厘斯（cSt）。

③数值多项式

式中，a、b、c同前；t为实际温度，℃；k为温度指数，一般k＝1。应用上面三种模型式（1．22）～式（1．24），关键是确定方程的三个未知系数a、b、c。直接插值法最为简便，但误差较大。最小二乘法一般只适合多项式形式。但需事先确定常数c，可用直接插值法求得。关于式（1．23）中的c值，一些石油类书籍中常数：c＝0．6。通过大量计算表明，这种将c值取为定值的做法并不可取。通过大量计算还发现，重对数式（1．23）易造成数值错误，使得计算结果不正确，而指数式（1．22）既简单实用，精度也很高，因此，推荐使用指数型黏温关系式作为黏温特性的基本方程。

在式（1．22）中，令：Y＝lnν，A1＝lna，A2＝b，X＝1／（t－c），则式（1．22）即可化为线性回归方程式。其中，c可以用三个实验数据直接插值得到。

2）常见液体和石油产品的黏温特性

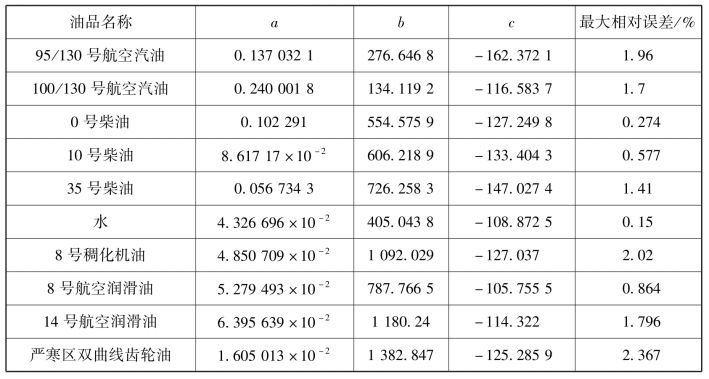
表1．5给出了部分流体指数型黏温特性方程的三个计算参数。其中运动黏度ν的单位为cSt。

表1．5　部分流体指数型黏温特性方程的a、b、c值