前已介绍流体平衡时不存在切应力的作用，一旦有微小剪切力的作用，就会发生连续变形。也就是说，在流动的流体内，流体层间必然存在剪切力（内摩擦力）的作用，以阻抗流体微团的变形，流体的这种性质称为黏滞性（黏性）。黏性可定义为：在流动的流体内部抗拒各流层之间作相对运动时产生内摩擦力的性质。

黏度产生的原因主要有：①分子之间的内聚力；②流体与固体壁之间的附着力；③分子之间的动量交换。液体主要是前两个原因，气体主要是最后一个原因。

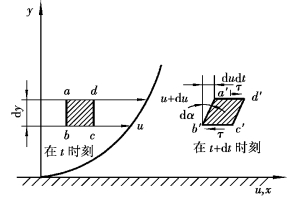
图1．1　黏性流体流动的剪切变形

黏滞性是流体的一个重要物理性质。图1．1表示了一简单流动情况。它是流体作层流流动时沿y方向实测得到的速度分布曲线（层流流动见第6章6．2节）。在壁面上，由于附着力的作用，流体质点黏附于壁面上，速度为零。稍离壁面，流体质点虽发生运动，但由于黏滞性的作用，速度还较小，离开壁面越远，速度越大。这表明各流体层间发生了相对运动，因而在各流体层接触面上产生了摩擦力。运动较快的流体层带动运动较慢的流体层，运动较慢的流体层阻滞运动较快的流体层。在这样的运动中，在t时刻呈正长方形abcd的流体微元，到t＋dt时刻，在x轴方向变形为a′b′c′d′。流体微元变形是内摩擦力发生作用的结果。

该摩擦力的大小与流体的黏性大小和层间的速度差异程度有关。根据牛顿的总结：两相邻流层之间摩擦力的大小T与接触面积A成正比，与速度梯度成正比，与流体的黏性有关，与压强无关。其数学表达式为

式中，μ称为动力黏度。它定义为(www.daowen.com)

在一点的变形率被定义为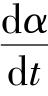，由图1．1可得

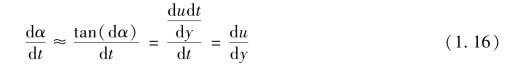
式中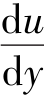， 称为速度梯度。由式（1．16）可见，切应变率（也称角变形速度）也可理解为速度梯度。

将式（1．15）和式（1．16）合并，并用μ表示动力黏度，τ表示切应力，牛顿内摩擦定律也可写为

上式表明，切应力与速度梯度和流体的黏滞性（黏度）成正比。