将在ANSYS中计算完成后包含有限元网格数据以及振动数据的.“rst”文件直接导入到LMS Virtual.Lab中，即可查看每个频率下的振动位移数据。将Pro/E中建立的外壳三维实体模型导入到CAE前处理软件Hypermesh中划分声学边界元网格（2D面网格图略），然后将其导入到LMSVirtual.Lab中。

结构的有限元网格与声学边界元网格并不相同，需要分别导入。两种网格在划分时使用了不同的顺序编号，会发生节点和单元编号冲突，这时需改变其中一种网格节点和单元的编号。本文结构有限元网格包含了ANSYS分析结果中的振动数据，故只能改变声学网格中发生编号冲突的节点和单元编号。导入两种网格后将网格类型分别定义为结构网格和声学网格，同时生成包络网格以定义边界条件。选择空气作为流体的材料属性，并将此属性赋予声学网格。

为了建立数据之间的耦合关系，即将有限元网格的振动数据转移到声学网格上，采用LMSVirtual.Lab软件中Maximum Distance算法，进行两种网格之间的数据映射，并将转换后的振动位移定义为边界条件进行声学间接边界元数值计算，结果如图8.4所示。

图8.4所示为不同频率声压分布云图。由图可知，不同频率时声压级分布规律相似，外壳辐射的球面上均为靠近圆形外壳两侧向下位置声压级较高，且进料口一侧声压级最高（图8.4d）。这是由于抛送装置内脉动气-固两相流场作用到圆形外壳两侧板上的法向压力较大，且进料口处由于气流转向会产生涡流，使得脉动气流波动幅度较大的缘故。出料管出料口附近声压级较高，原因是出料口处气动噪声较大^[110-111]，使得出口管壁振动也较大，故产生较高的振动辐射噪声。由图8.4可见，激振基频100Hz时，A计权最大声压级为85.90dB（A）（图8.4a，未经过A计权的最大声压级为105.80dB，略）；2倍频200Hz时，A计权最大声压级88.64dB（A）（图8.4b，未经过A计权的最大声压级为99.54dB，略）；3倍频300Hz时，A计权最大声压级为86.48dB（A）（图8.4c，未经过A计权的最大声压级为93.58dB，略）；4倍频及以后倍频噪声非常小，忽略不计。由于未经过A计权的声压级表征的是叶片式抛送装置振动辐射噪声的大小，比较可知，激振基频100Hz时振动辐射噪声最大，200Hz时振动辐射噪声次之，300Hz时较小。这和外壳振动响应分析结果基本一致，可见振动辐射噪声数值预测结果合理。A计权声压级是考虑人耳对噪声的主观感受通过频率计权网络确定的声级，频率越低，A计权声压级衰减越严重，故A计权后200Hz时声压级最大，300Hz时次之，基频100Hz时最小。假定接收场点为球面，则其半径为2.041m，可求得抛送装置的声功率级为95.04dB（A）。(www.daowen.com)

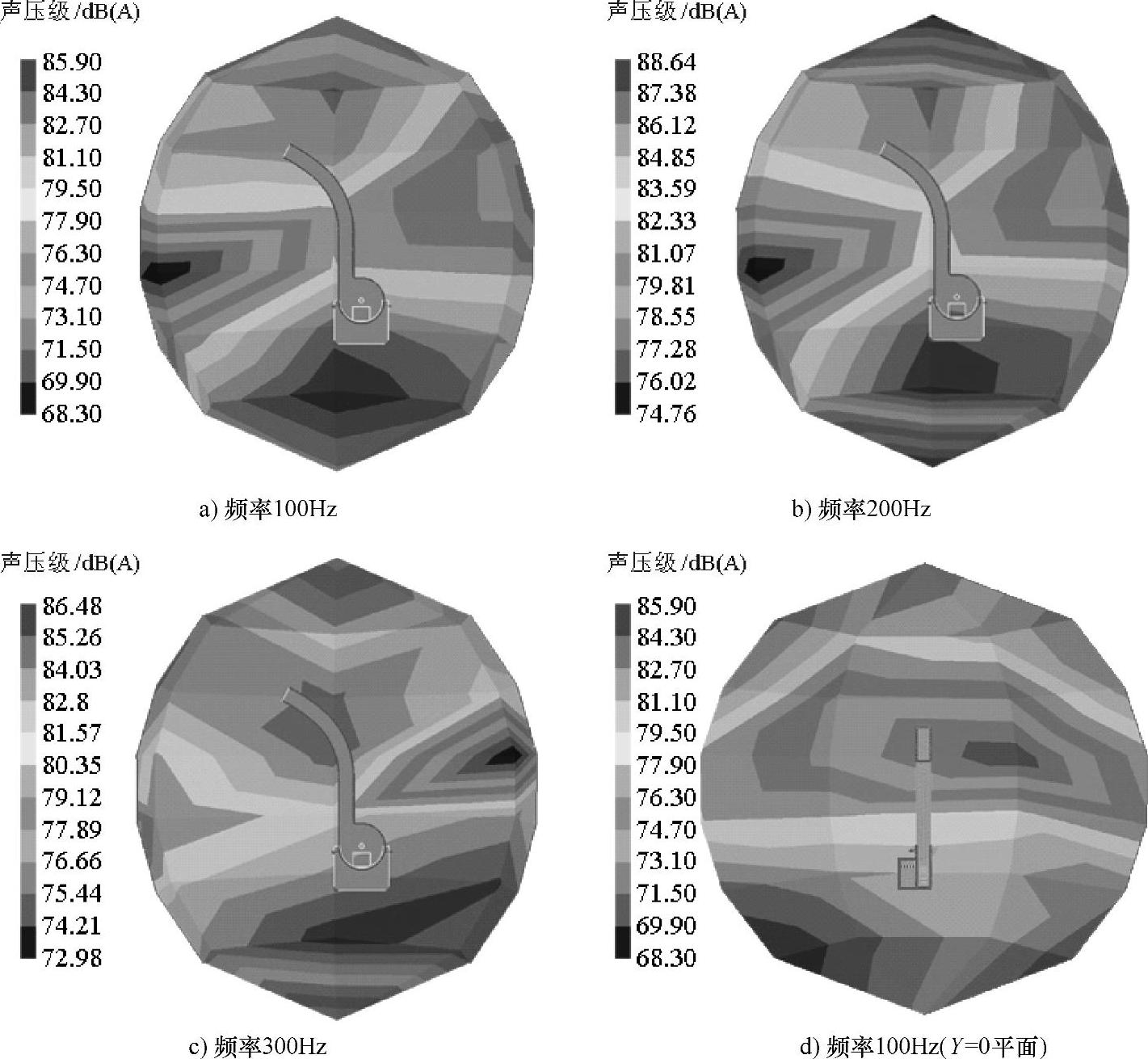
图8.4 抛送装置外壳辐射噪声声压级分布云图