为了研究加入物料对叶片式抛送装置气流流场及气动噪声辐射规律的影响，对叶片式抛送装置进行气固两相流场数值计算。为了更好地模拟玉米秸秆颗粒对气流流场的影响，本节采用稠密离散相模型（Dense Discrete Phase Model，DDPM）模拟抛送装置内气固两相流场。稠密离散相模型综合了欧拉-欧拉方法（欧拉模型）和欧拉-拉格朗日方法（离散相模型）的优点，可以进一步提升气固两相流场数值计算求解精度。

1.气固两相流场数值模拟

在本章7.2.2节中已经对叶片式抛送装置流场进行了基本的设定，且气流场和气固两相流场数值模拟采用同一套网格，为简化计算过程本节直接导入7.2.2节的非稳态“cas”文件，再进行后续设置和计算。

（1）求解参数设定

1）求解模型。求解器仍采用压力差值格式非定常求解器，在应用稠密离散相模型时，需要设定多相流模型、湍流模型及离散相模型。多相流模型采用隐式欧拉模型，并开启稠密离散相模型，设定离散相个数为1。湍流模型采用精度更高的大涡模拟模型，大涡模拟相关选项采用默认值。壁面的流动模拟采用标准壁面函数，多相流湍流模型采用混合模型。离散相模型中考虑离散相与连续相之间的耦合作用；设定每100步连续相计算便做一次离散相的干扰计算；为完整追踪物料颗粒运动轨迹，设定最大追踪步数为50000步；定义物料颗粒从物料入口面沿法向进入，速度为15m/s、平均粒径为0.0135m、流量为0.5kg/s，其他参数使用默认值。

2）求解离散格式及求解项松弛因子。压力-速度耦合方式采用Phase Coupled SIMPLE算法，梯度离散格式采用Green-Gauss Node Based格式，动量、体积分数、湍动能和耗散率的离散格式均采用一阶迎风格式；压力项和动量项松弛因子设为0.2，其余各项松弛因子均采用默认值。

（2）物理问题设定 环境参数和流体域参数的设定仍沿用气流流场求解设定，边界条件在沿用气流流场求解设定的基础上接受软件默认修改，其他参数修改如下：

1）材料属性。流体材料仍沿用空气，修改惰性粒子的名称为“wuliao”，密度为玉米秸秆颗粒的实际密度92.1kg/m³。

2）物相属性。主相（连续相）为空气；离散相为物料并开启颗粒定义项，设置颗粒动力黏度项采用gidaspow方法获得、颗粒体积黏度项采用lun-et-al方法获得，其他参数采用默认设置。

（3）迭代监控设定及求解 开始计算前，需要对流场进行初始化，本节选用混合初始化方法进行初始化操作，并重置离散相源项。迭代监控仍沿用残差监控和出口流量监控。时间步长不变，每个时间步长的最大迭代步数设置为30。以上述设置参数对叶片式抛送装置内三维非定常气固两相流场进行数值仿真。迭代计算稳定后，每个时间步长迭代15次左右收敛，进行下一个时间步长的计算。气固两相流非定常流场数值计算残差如图7.20所示，残差图的波动稳定且规律，同时气固两相流非定常流场数值计算出口流量波动较小且稳定，具有周期性，所以迭代计算收敛。(www.daowen.com)

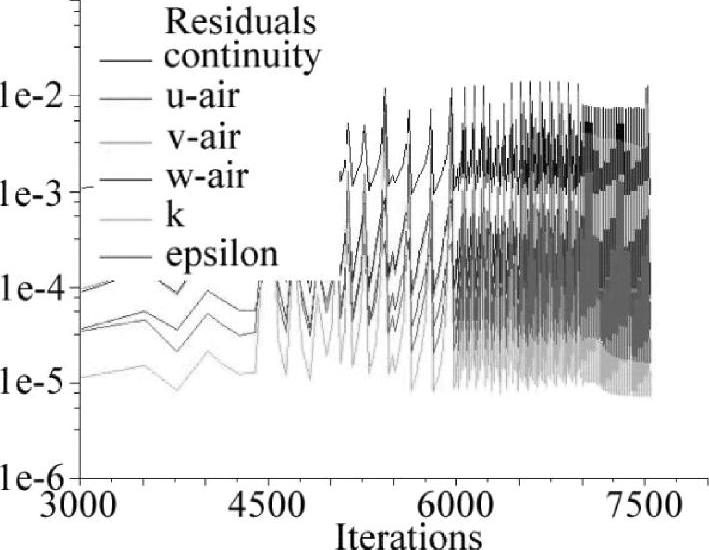
图7.20 气固两相流非定常流场数值计算残差

2.负载两相流流场计算结果分析及压力数据输出

为了获得叶片式抛送装置内气固两相流场特性，对仿真求解结果进行后处理，分析其总压、静压、动压及速度矢量的分布特点。对仿真结果进行后处理时，仍沿用过原点三个相互垂直的截面（即X=0截面、Y=0截面及Z=0截面）。通过分析仿真结果后处理云图，获得抛送装置内流场分布特性。同时，分析加入物料对抛送装置内流场特性的影响。

对转速为1500r/min、叶片数为4、叶片倾角为0°、进料口尺寸为200mm×160mm、无出料直管时的叶片式抛送装置内气固两相流场数值模拟结果进行后处理，得到三个截面处混合相的静压云图（图7.21a）、空气相的总压云图（图7.21b）、空气相的动压云图（图7.21c）及空气相的速度矢量图（图7.21d），并对其变化规律进行分析。

对比图7.21a和图7.2b可知，加入物料后抛送装置内的静压值升高，且加入物料后出料管内的静压分布更均匀。这主要是由于加入物料后占据了一定的空间体积，并和空气相互挤压的缘故。对比图7.21b和图7.2a可知，加入物料后抛送装置内空气相总压的最大值降低而最小值升高。对比图7.21c和图7.2c、图7.21d和图7.2d可知，加入物料后抛送装置内空气相动压和速度矢量的分布更为均匀，且动压及速度的最大值降低而最小值均明显升高，动压和速度的分布更集中。这主要是由于加入物料后，低于气流速度的物料对气流运动的阻碍作用使气流速度及动压的最大值降低，同时部分物料由于获得叶片抛扔的能量使得气流速度及动压的最小值明显升高的缘故。而动压最大值下降较静压最大值升高更多，故加入物料后空气相的总压变化规律与动压及气流速度变化规律一致。

加入物料后流场脉动压力数据的输出方式与7.2.3节相同。

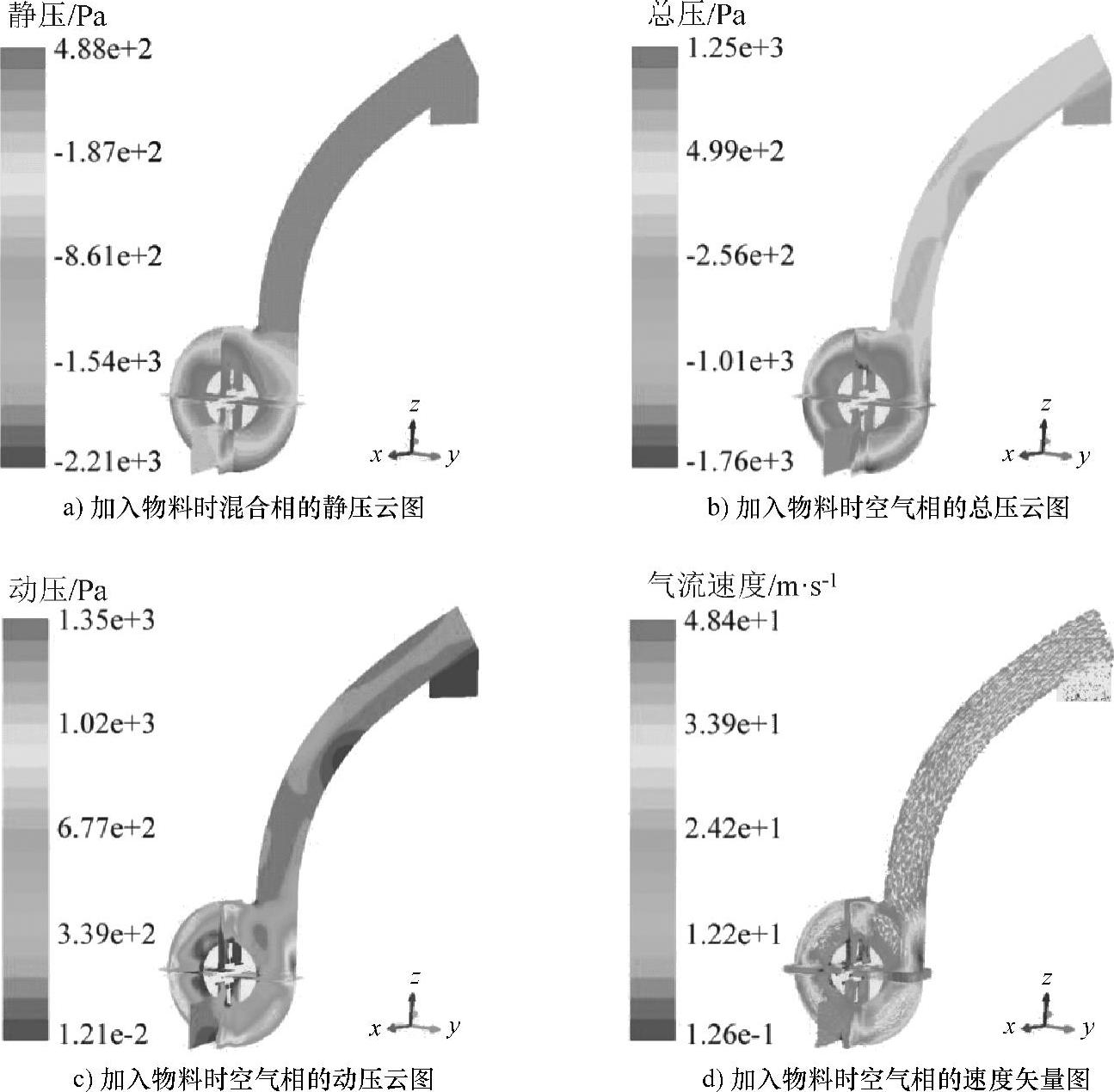
图7.21 抛送装置内气固两相流场数值计算结果云图