（1）显著性分析 利用Design Expert 8.0软件中的ANOVA方差分析功能，以表6.4中的架板半径、叶片厚度、架板厚度（即A、B、C）为研究因素，以前三阶预应力模态频率值（即P₁、P₂、P₃）为响应值进行多元回归分析，通过F检验判定回归方程中各个变量影响响应值的显著性。方差分析结果分别见表6.6、表6.7和表6.8。

表6.6 P₁方差分析结果

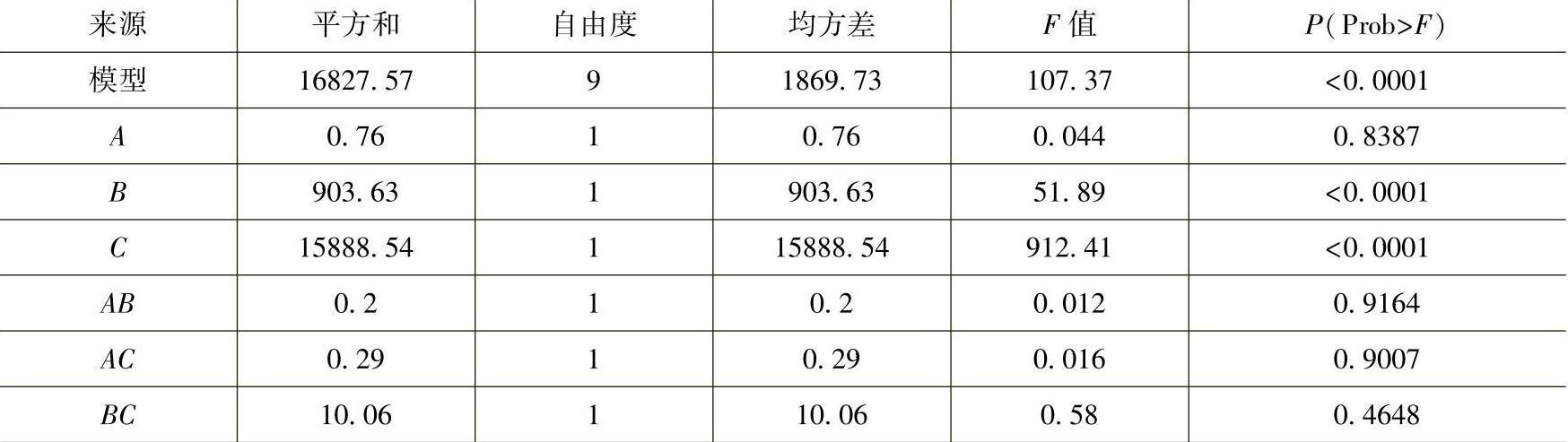
（续）

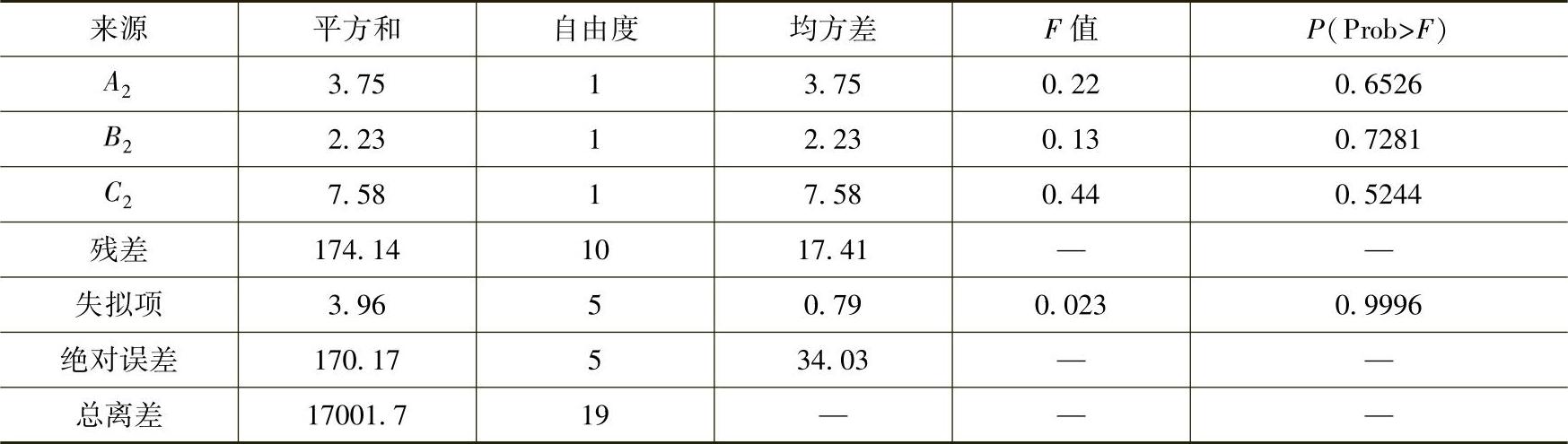
从表6.6可以看出，架板厚度和叶片厚度对预应力模态第一阶频率值影响显著，架板半径影响不显著；交互项的P值都大于0.05，说明交互项对预应力模态第一阶频率的影响不显著。

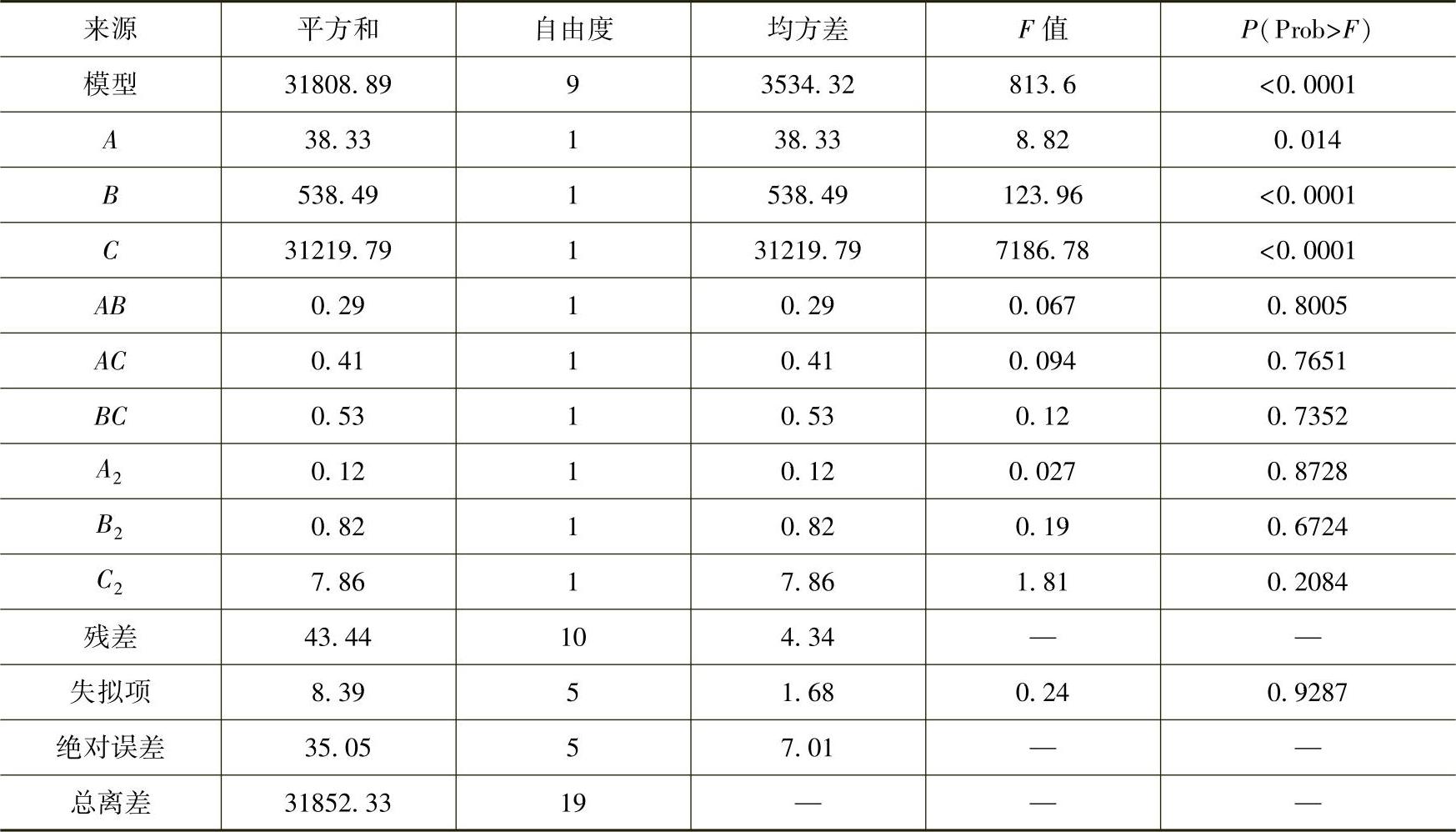
表6.7 P₂方差分析结果

模型通过F检验的P值小于0.0001（P<0.01，影响极其显著），表明对响应值P₁的影响极其显著；失拟项F检验的P值为0.9996，大于0.05，失拟不显著，表明无失拟因素存在，对模型是有利的。回归方程的复相关系数R²=0.9992，表明该模型的拟合情况良好，回归方程的代表性较好，其校正系数R²_adj=0.9981，表明该模型解释了99.81%效应值变化，试验误差很小，回归方程能够很好地描述各变量与响应值的线性关系，利用该模型可以模拟预测最优条件。

从表6.7可以看出，架板厚度和叶片厚度对预应力模态第二阶频率值影响显著，架板半径影响不显著；交互项的P值都大于0.05，说明交互项对预应力模态第二阶频率的影响不显著。

模型通过F检验的P值小于0.0001，表明对响应值P₂的影响极其显著；失拟项F检验的P值为0.9287，大于0.05，失拟不显著，无失拟因素存在。回归方程的R²=0.9993，模型的拟合情况良好，回归方程的代表性较好，校正系数R²_adj=0.9984，表明该模型解释了99.84%效应值变化，试验误差很小，回归方程能够很好地描述各变量与响应值的线性关系。

表6.8 P₃方差分析结果(www.daowen.com)

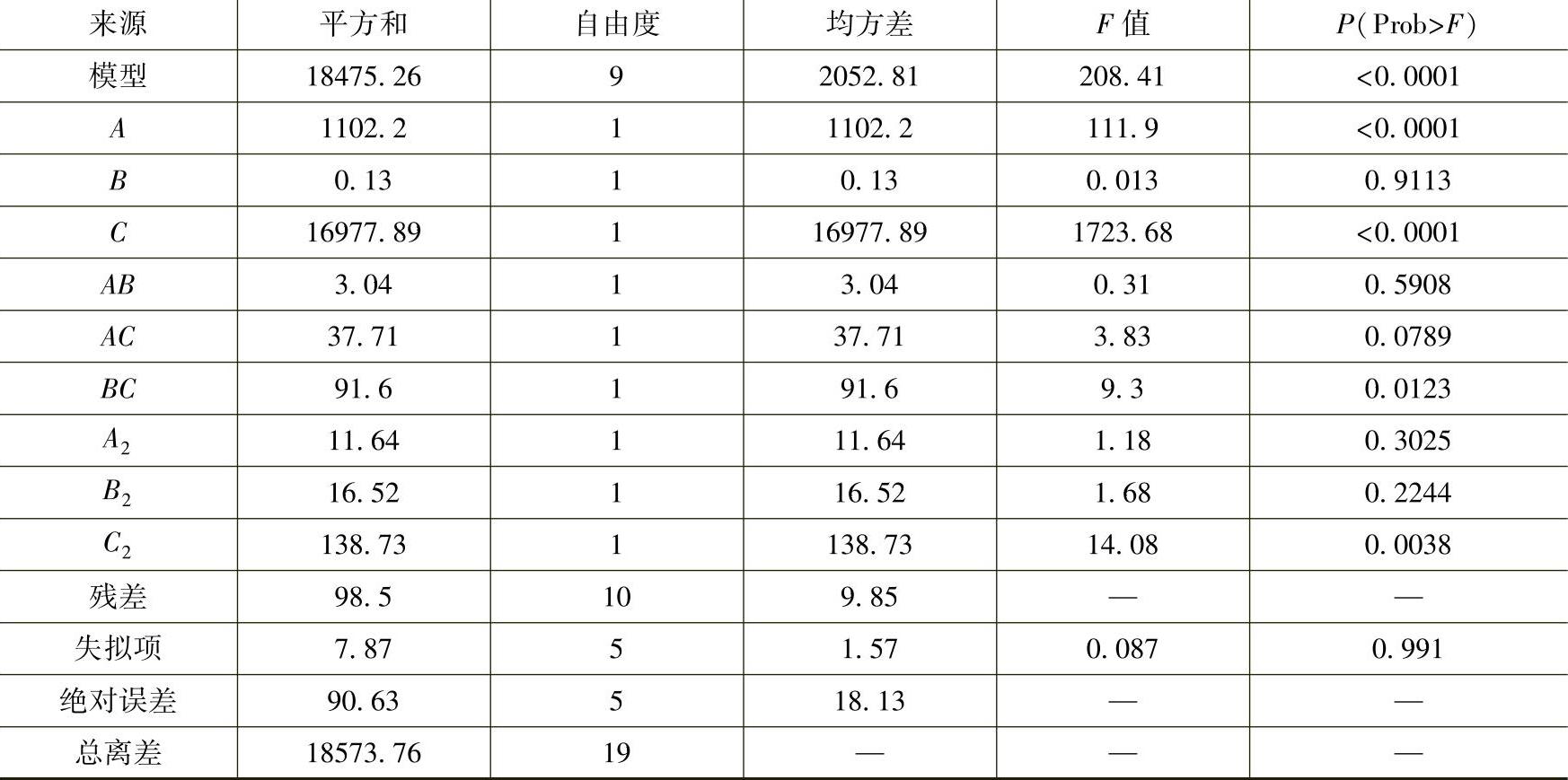
从表6.8可以看出，架板厚度和架板半径对预应力模态第三阶频率值影响显著，叶片厚度影响不显著；交互项BC的P值小于0.05，而交互项AB和AC的P值都大于0.05，说明叶片厚度和架板厚度的交互作用对预应力模态第三阶频率的影响显著，架板半径和叶片厚度的交互作用及架板半径和架板厚度的交互作用对预应力模态第三阶频率的影响不显著。

模型通过F检验的P值小于0.0001，对响应值P₃的影响极其显著；失拟项F检验的P值为0.991，失拟不显著。复相关系数R²=0.9992，表明该模型的拟合情况良好，校正系数R²_adj=0.9982，表明该模型解释了99.82%效应值变化，试验误差很小，回归方程能够很好地描述各变量与响应值之间的线性关系。

（2）优化结果分析 多因素响应面优化法，是以响应值（如预应力模态频率、几何质量等）为因变量，多个因素（如叶片厚度、叶片长度等）为自变量建立函数关系。优化输出参数与多个输入参数的回归关系可表示为曲线或曲面。

如图6.41所示，预应力模态前三阶频率随架板厚度增加呈线性增大的趋势（图6.41a、d和g）；随着叶片厚度的增加，前两阶频率呈线性减小的趋势，第三阶频率先增大后减小（图6.41b、e和h）；随着架板半径的增大，前两阶频率逐渐减小，第三阶频率逐渐增大（图6.41c、f和i）。总体上架板厚度对预应力模态低阶频率影响程度最大，叶片厚度次之，架板半径影响程度较小。

Workbench优化系统依据不增加几何质量提高前三阶固有频率避开率的优化目标，生成三个备选设计点，见表6.9。结合响应曲线分析结果，可以看出第三个备选设计点即叶片厚度为4.24mm，架板半径为109.89mm，架板厚度为11.55mm更为合理，有效地实现了优化目标，使抛送叶轮的预应力模态第一阶频率与基频激振频率的避开率由21.98%提高到35.82%，叶轮的预应力模态第二阶频率与2倍频激振频率的避开率由8.76%提升到11.11%，叶轮的预应力模态第三阶频率与3倍频激振频率的避开率由4.27%提升到7.55%，叶轮总质量减小了2.85%，节约材料的同时提升了装置的动态特性。

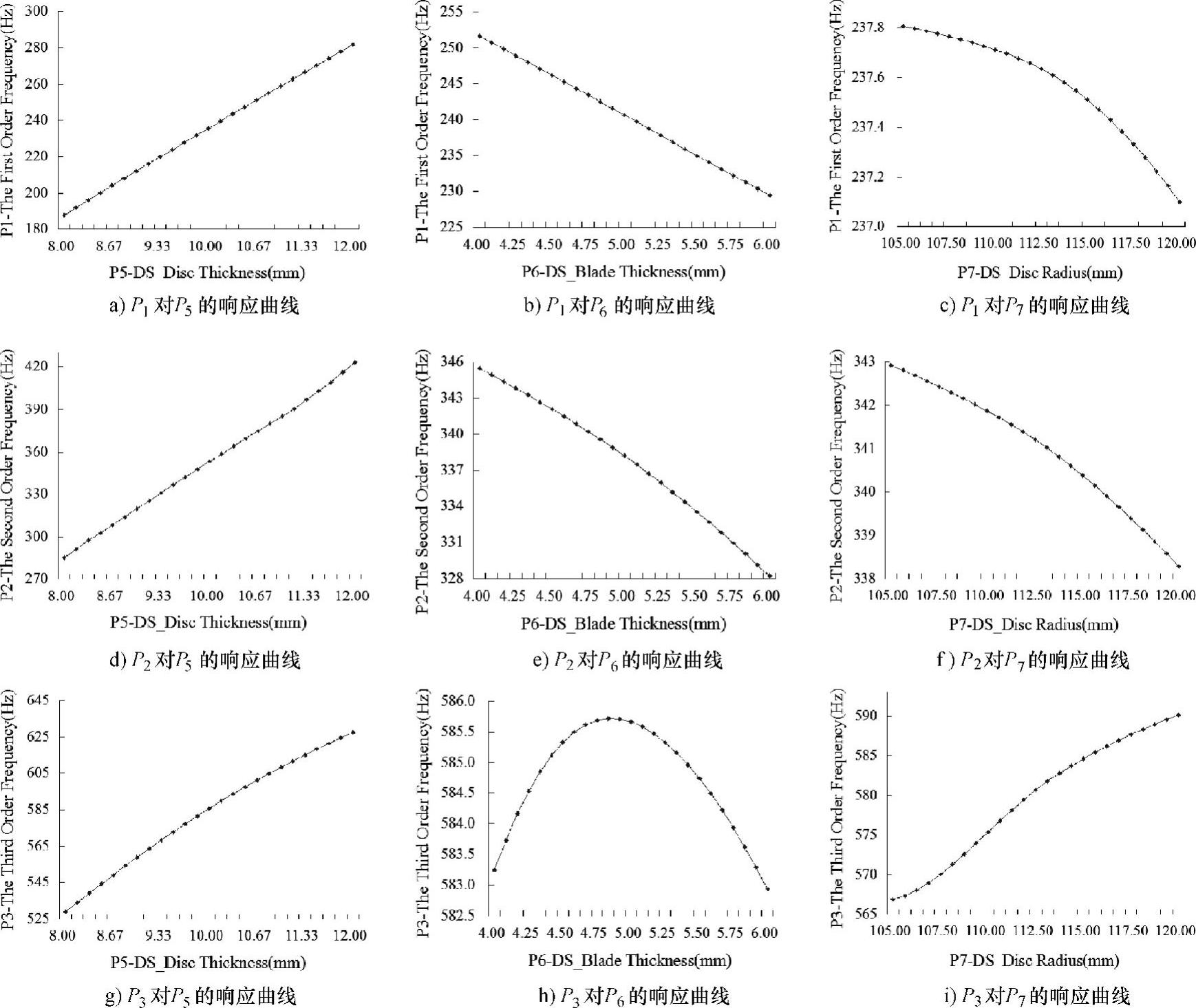
图6.41 输出参数对输入参数的响应曲线图

表6.9 备选设计点