利用哈密尔顿（Hamilton）原理建立结构整体的运动方程。考虑叶片式抛送装置内气固两相流场对叶轮的作用，在流体中离散后弹性体的结构动力学方程为[77]

式中 M——质量矩阵；

C——阻尼矩阵；

K——刚度矩阵；u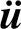，，——节点的位移矢量、速度矢量和加速度矢量；

F——节点所受的合力（N），包括自身重力、离心力和流场的压力。

对式（6.10）进行拉普拉斯变换可得

（s²M+sC+K）u（s）=F（s） （6.11）

式中 s——变换因子；

u（s）和F（s）——u和F的拉氏变换。

对线性非时变系统，其极点在复平面左半平面，因此可将s变换为jω，则叶轮运动方程为

（-ω²M+jωC+K）u（ω）=F（ω） （6.12）

系统的任一点响应均可表示为各阶模态响应的线性组合。任一l点的响应可表示为

式中 ω——频率（Hz）；(www.daowen.com)

φ_lr——l点处第r阶模态振型系数；

q_r（ω）——第r阶模态坐标，即r阶模态对响应的贡献量。

由N个测点的模态振型系数组成的列向量ϕ_r称为第r阶模态向量，它反映该阶模态的振型。由各阶模态向量组成的矩阵（N×N阶）为模态矩阵，表示为

Φ=[ϕ₁…ϕ_r…ϕ_N] （6.14）

由式（6.13）和式（6.14）可得系统的响应列向量为

u（ω）=ΦQ （6.15）

其中，Q=[q₁（ω）…q_r（ω）…q_N（ω）]^T

将式（6.15）代入式（6.12），再左乘Q^T，可得

（-ω²[M_r]+jω[C_r]+[K_r]）Q=[F_r] （6.16）

式中 [M_r]、[C_r]、[K_r]、[F_r]——对角矩阵。

由ω²_r=K_r/M_r，即可求出各阶模态的固有频率^[78][79]。