1.疲劳的概念

金属材料或零件在工作过程中受到循环变载荷的作用，各点的应力随时间做周期性的变化。这种随时间做周期性变化的应力称为交变应力或循环应力。在交变应力的作用下，虽然材料试件或零件所承受的应力低于材料的屈服强度，但经过较长时间的工作后产生裂纹或突然发生完全断裂的现象称为金属的疲劳。出现可见裂纹或者完全断裂都称为疲劳破坏。

美国实验与材料协会（ASTM）在“疲劳试验及数据统计分析之有关术语的标准定义”中将疲劳定义为在点或某些点承受扰动应力，且在足够多的循环扰动之后形成裂纹或完全断裂的材料中所发生的局部的、永久结构变化的发展过程称为疲劳^[64]。

造成零部件发生疲劳断裂有许多形式，由于受力方式的不同可分为弯曲疲劳、拉压疲劳、扭转疲劳和复合疲劳；由于零件工作环境的不同也可分为热疲劳、腐蚀疲劳和机械疲劳。

热疲劳是由于零件工作时所处环境存在温度的反复变化，从而引起应变的循环变化。发生热疲劳必须有温度反复变化和机械约束两个必备条件的共同作用。由于材料的热胀冷缩特性，当零件所处温度发生变化时，零件自身产生约束力，称为热应力。腐蚀疲劳是指零件在腐蚀与交变循环载荷共同作用下产生的断裂现象，零件发生疲劳断裂是由于机械零件被腐蚀，破坏了原有的材料属性引起的。机械疲劳是交变载荷作用下发生的破坏现象。机械疲劳是由单纯的循环变载荷作用引起的，材料本身没有受到温度变化及环境影响^[65-66]。

按照在一定应力作用下循环次数的不同又可以分为高周疲劳和低周疲劳。低周疲劳的循环应力接近或超过了材料的屈服极限，塑性应变起主导作用，疲劳破坏循环次数一般低于10⁴～10⁵，此时疲劳寿命较短，称为应变疲劳或低周疲劳。高周疲劳应力较小，低于材料的屈服极限，处在材料的弹性极限范围内，弹性应变起主导作用，疲劳破坏循环次数一般高于10⁴～10⁵，此时疲劳寿命较长，称为应力疲劳或高周疲劳。

2.疲劳累积损伤理论

零件发生疲劳断裂是由于零件承受循环变载荷作用引起的，断裂的产生是载荷不断叠加的结果。零件所受载荷的叠加理论主要有非线性累积损伤理论和线性累积损伤理论。非线性累积损伤理论考虑零件受到载荷间的相互作用，不是单纯地将零件所受不同载荷所产生的疲劳损伤叠加。非线性累积损伤理论常用的疲劳破坏准则为Carten和Dolan提出的Carten理论。Carten理论考虑了应力之间的相互影响，每次计算损伤都要考虑本次循环载荷之前载荷系列中最大载荷的作用，要实时求得损伤。故应用此理论计算疲劳精度较高，但应用过程难度较大，在工程计算中使用较少。线性累积损伤理论单纯地将零件所受不同载荷造成的疲劳损伤进行叠加，线性累积损伤认为零件所受各载荷作用都是相互独立的，不考虑力与力间的相互作用，将各载荷造成的疲劳损伤叠加到材料所能承受的临界值时即认为发生疲劳损坏。由于线性累积损伤理论应用简单，故在工程中广泛使用。叶片式抛送装置抛送叶轮主要承受离心力、流场力以及重力等载荷，所受载荷间相互影响较小，故选用线性累积损伤理论。线性累积损伤中最为典型的代表就是Palmgren-Miner理论，简称为Miner理论^[67-68]。

工程中Miner理论应用广泛，该理论认为：

1）对于等幅应力水平S作用下的构件，一次循环造成的损伤为

式中 N——对应于当前应力水平S的疲劳寿命。

2）对于等幅应力水平S作用下的构件，n次循环造成的损伤为

当n=N时，D=1，构件发生疲劳破坏。

3）对于变幅应力水平作用下的构件，假设构件承受k种不同的应力水平作用，在应力水平S_i作用下经过n_i次循环，对应等幅应力水平S_i的疲劳寿命为N_i。则每一次循环造成的损伤为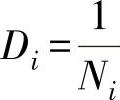，ni次循环造成的疲劳损伤为D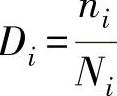，用D_i来衡量各应力水平循环作用下造成的损伤，当这些损伤累积起来等于1时，将会发生疲劳破坏，疲劳破坏准则为

式中 N_i——在应力水平S_i作用下到疲劳破坏的寿命，由S-N曲线确定。

Miner线性累积损伤理论并没有考虑到应力水平S_i作用的先后顺序。

3.材料的S-N曲线(www.daowen.com)

材料的疲劳特性可用最大应力σ_max、应力循环次数以及应力比r来描述。机械零件材料的抗疲劳性能是通过试验测定的，即在材料的标准试件上加上一定应力比的等幅变应力，通常是加上应力比r=-1的对称循环应力或r=0的脉动循环应力，通过试验，记录在不同最大应力下引起试件疲劳破坏所经历的应力循环次数N。以最大应力或应力幅S为纵坐标、以循环次数N为横坐标用图形来表达试验结果，就可得到材料的疲劳特性曲线^[69]。疲劳失效以前所经历的应力循环次数N又称为疲劳寿命，表示最大应力或应力幅S与疲劳寿命N之间关系的曲线称为疲劳寿命曲线或S-N曲线。

材料的S-N曲线通常由试件在各种载荷（拉、压、弯曲、扭转等）作用下通过试验获得。S-N曲线包括弯曲应力与循环次数的σ-N曲线及扭转切应力与循环次数的τ-N曲线。

S-N疲劳寿命曲线在直角坐标系上是一条双曲类型的曲线，如图6.29a所示，其表达式为

NS^m=C （6.8）

式中 m和C——材料常数。

将式（6.8）两边取对数可得

lgN=lgC-mlgS （6.9）

由式（6.9）可知，S-N曲线在双对数坐标上为一条直线，1/m为其负斜率。分别在直角坐标系及双对数坐标系中绘制的S-N曲线如图6.29所示^[67，70]。

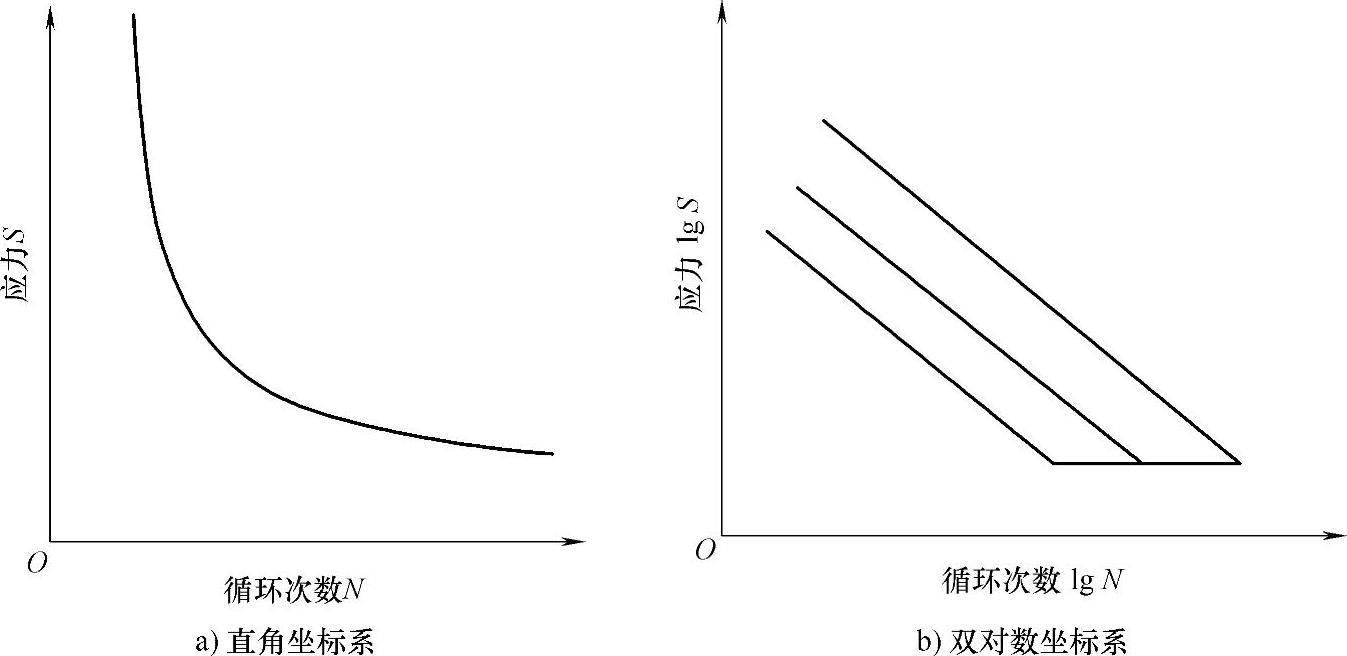
图6.29 S-N曲线示意图

4.疲劳的影响因素

（1）平均应力的影响 通常反映材料疲劳性能的S-N曲线是在做材料疲劳试验时加载平均应力σ_m=0、应力比r=-1的对称循环应力获得的。但在叶片式抛送装置实际工况下，抛送叶轮是在高应力水平下运行的，平均应力σ_m≠0（图6.28），平均应力不同，其疲劳极限也不同，这就需要考虑平均应力对材料疲劳性能的影响，进而对原有的S-N曲线进行修正。材料的疲劳极限应力线图（又称等寿命疲劳曲线）的横坐标是平均应力σ_m，纵坐标是应力幅σ_a。目前主要的修正曲线有古德曼（Goodman）直线、戈倍尔（Gerber）曲线、折线（Floder line）以及索德倍尔（Soderberg）直线^[71-72]。四种曲线样式如图6.30所示。

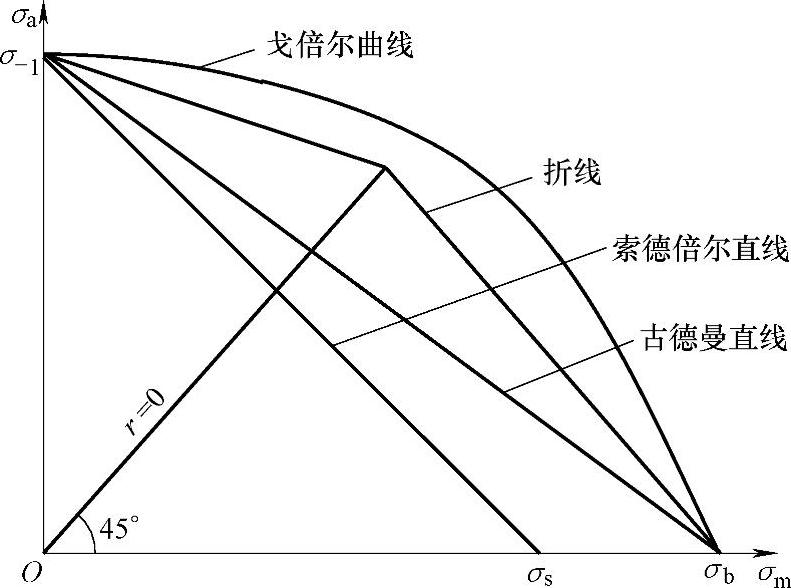
图6.30 极限应力线图

由图6.30可以看出，在较低应力水平下，索德倍尔直线模型太保守；戈倍尔抛物线模型不仅计算复杂而且比较危险。折线模型和古德曼直线模型比较适合。由于在Workbench中没有折线模型，所以采用古德曼直线模型来估算疲劳强度与疲劳寿命^[63]。

（2）应力集中的影响 实际结构产生失效的主要原因之一是存在应力集中现象，在工程设计领域一直被认为是导致结构失效的主要因素之一。通过对试件进行试验可知结构发生疲劳断裂的部位往往也是出现应力集中的部位，应力集中现象降低了结构的整体抗疲劳性能。抛送叶轮设计时存在一些孔及台阶等结构，会产生应力集中现象，在循环变载荷长时间的作用下极易发生疲劳破坏。

（3）尺寸的影响 在受相同载荷作用时尺寸较大的结构所受高应力的范围也越大，产生疲劳破坏的可能性也就越大。其原因是结构尺寸大时，材料晶粒粗，出现缺陷的概率大，机械加工后表面冷作硬化层相对较薄，疲劳裂纹容易形成。故尺寸较大的结构反而更容易发生疲劳断裂。

（4）表面加工状况的影响 疲劳裂纹总是最先出现在构件的表面，一方面是由于构件表面所受应力较大且表面缺陷相对较多；另一方面是由于材料表面的约束较小，容易产生滑移现象。因此，零件表面加工状况的好坏在一定程度上对疲劳强度有影响。零件表面状况的好坏可以通过零件表面粗糙度、所受应力情况及零件表面组织特性决定。零件的加工表面越光滑，缺陷也就越少，越不容易产生应力集中，疲劳强度也就越高。还可以通过对零件表面进行处理来改变零件的表面组织特性，提高零件表面的疲劳强度^[73-74]。