1.抛送叶轮有限元模型建立
理论上,为了得到准确的有限元分析结果,不需要对有限元模型进行简化,但实际工程分析中,复杂模型、多分析步数、多载荷种类等都会较大地增加计算机负荷,因此在保证计算精度的前提下,有限元模型可以适当地简化。
为保持模型的一致性,抛送叶轮仍使用流场计算所建立的三维实体模型。抛送叶轮的网格划分在ANSYSMeshing应用程序中进行,生成包含节点和单元的有限元模型,抛送叶轮网格数为27825,如图6.5所示。结构网格划分物理环境为Mechanical,关联中心默认值粗糙;平滑度为中等,过渡为快,设置局部尺寸控制,在叶轮几何物理量变化大的部位细化网格。
划分完网格后有必要对网格的质量进行检查,网格质量的检查功能通过Statistics>Mesh Metric来完成。常用的网格质量检查工具为单元质量(Element Quality),衡量准则为网格边长比,单元质量值越接近1网格质量越好。叶轮网格的单元质量为:0.38~0.63的网格数占12.04%,0.63~1的网格数占87.96%,说明叶轮网格质量符合计算要求。
2.设置材料属性加载求解
(1)添加材料属性 试验台抛送叶轮所用材料为普通碳素结构钢Q235,其材料特性相关参数见表6.1。

图6.5 叶轮结构网格
表6.1 材料特性参数
Workbench中由Engineering Data控制材料属性,材料库中保存了大量常用材料数据,选中Structural Steel材料可进行材料属性值的修改,设置材料密度为7.8×103kg·m-3,弹性模量为2.06×1011Pa,泊松比为0.3,完成工程材料设定即可将其添加到分析项目中。
(2)施加载荷及约束 载荷与约束是Mechanical求解计算的边界条件,以所选单元自由度的形式定义。Mechanical中提供了惯性载荷、结构载荷、结构约束及热载荷4种类型的约束载荷。
抛送叶轮在设计工况下绕固定旋转轴以额定转速旋转,叶轮主要承受两种载荷:一种是惯性力,即叶轮旋转产生的离心力与重力;另一种是所抛送物料流及气流对叶轮的压力。两种载荷的作用效果不同,离心力导致叶轮受到拉伸作用,物料和气流对叶轮的压力导致其发生弯曲变形。
单向耦合过程中,直接将流场数值计算结果中抛送叶轮表面压力载荷加载到叶轮结构耦合面上,同时加载旋转离心力载荷以及叶轮自重,整个耦合计算过程在Ansys Workbench中实现。
离心力以体积力的形式分布于叶轮上,是迫使旋转的叶轮远离其旋转中心的力,它与质量、转速以及其所处的半径成正比。计算时,以定义旋转体力的形式将离心力施加到模型单元的质心上,方向向外,使整个模型以给定的速率(单位为每秒弧度)绕旋转轴转动,大小如下式所示:
PEi=mEiω2REi=ρVEiREiω2 (6.1)
式中 PEi——单元i所受的离心力(N);
ω——叶轮旋转的角速度(rad/s);
mEi——单元i的质量(kg);
ρ——叶轮材料密度(kg·m-3);
VEi——单元i的体积(m-3);
REi——单元i的质心距旋转轴心的距离(mm)。
由式(6.1)可以看出,只需给定旋转角速度和材料密度,有限元分析软件就可以计算得到各个单元的离心力。依据工况在Workbench中对抛送叶轮整体施加旋转速度(Rotational Velocity),设定叶轮轴轴向为Y轴,转向为正转,通过公式ω=2πn/60可由转速n计算出角速度ω。
物料和气流压力是分布在叶轮表面的一类载荷,由于物料和气流两相流场在实际运动过程中是不均匀的,所以在叶轮各部分结构上的物料和气流压力分布也不相同。定常数值模拟结果中的物料和气流压力数据通过Fluid Flow项目模块与Static Structural项目模块接口加载到抛送叶轮上,即流固耦合过程,结构模型上的压力根据表面对应进行加载。CFD分析所用的模型与静力分析的模型完全一致,加载流场压力时选中叶轮表面与CFD中Blade表面对应,流体分析得到的物料气流压力加载到叶轮上的匹配率为100%,如图6.6所示。

图6.6 物料和气流压力载荷
约束也称为边界条件,是建立模型区域之间或模型区域同它周围模型之间的关系,是指在运动边界上方程组的解应该满足的条件。根据叶轮的实际工作情况,需要对其X、Y、Z三个坐标轴方向的移动和绕X、Z轴的转动施加约束,仅保留绕Y轴转动的一个自由度,给定绕Y轴转动的转速后即可反映叶轮的实际工作状态。
3.抛送叶轮应力应变仿真结果分析
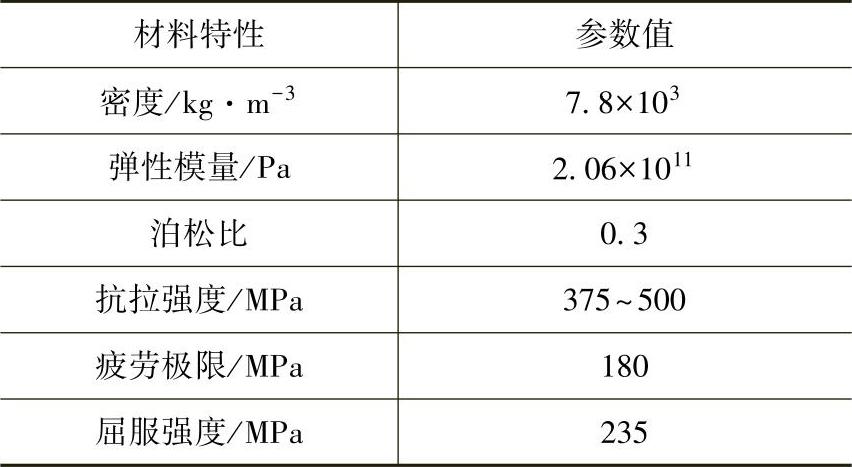
(1)空载与负载叶轮应力应变分析 空载抛送叶轮转速为1500r/min时,叶轮等效应力、等效应变及总变形云图如图6.7所示。
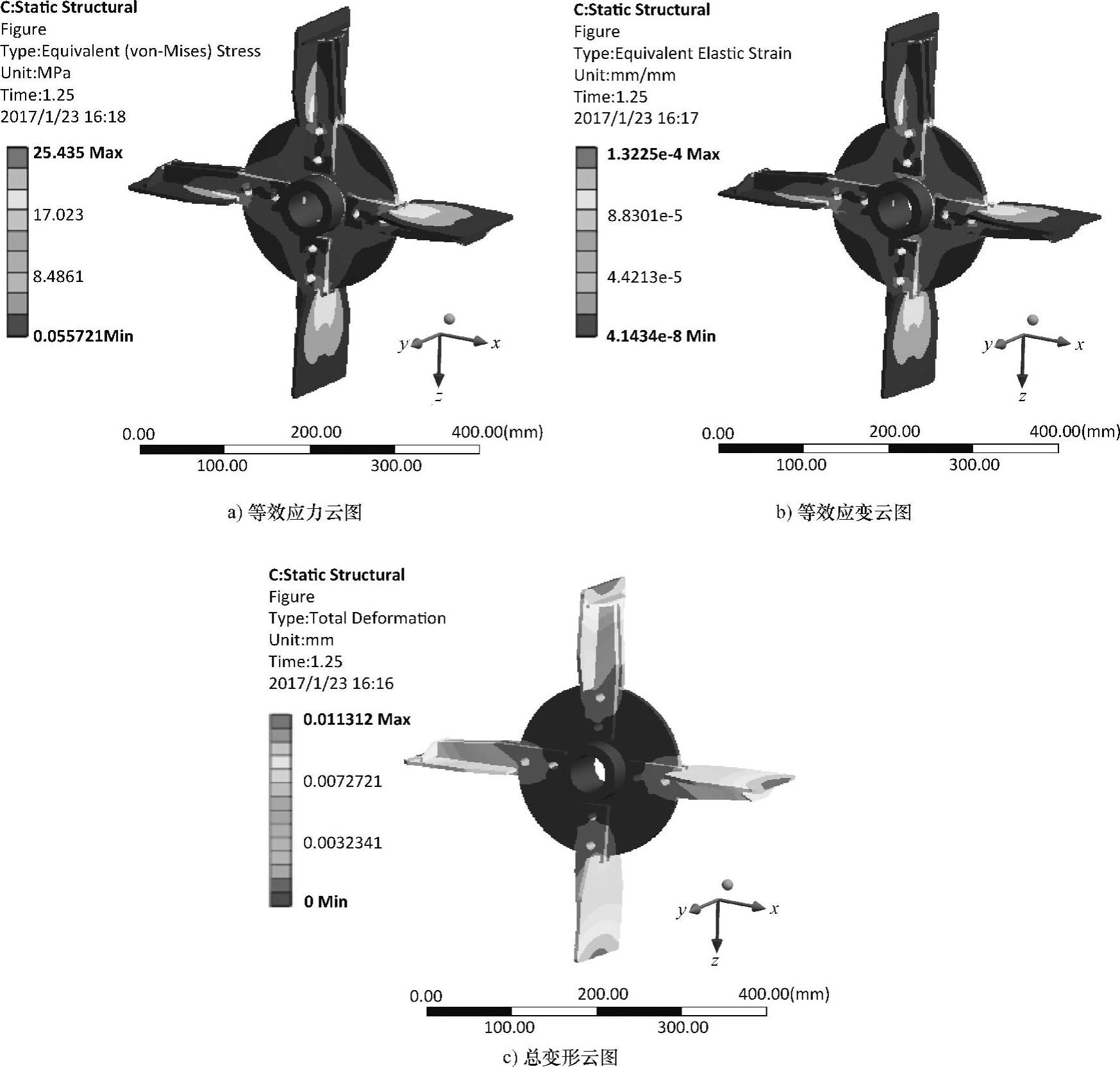
图6.7 空载抛送叶轮转速为1500r/min时,叶轮等效应力、应变及总变形云图
由图6.7a可知,最大等效应力出现在叶片与加强板连接的边缘处靠近叶片一侧;叶片与加强板和圆形架板连接处存在明显的应力集中,且附近区域应力较大,应力变化相对较快。这是由于物体几何外形在接合处变化剧烈以及物体厚度的差异造成的,在叶轮高速旋转的情况下这种现象更加显著。从应力云图还可以看出,叶片应力沿径向逐渐减小,外端应力最小;沿轴向叶片应力大小由中心向两侧逐渐减小,且两侧应力对称分布。
从图6.7b所示的应变云图可以看出,应变与应力的变化趋势相同,最大应变位置同样是在叶片与加强板和圆形架板外边缘连接处。
由图6.7c所示的总变形云图可知,叶片的外边缘位置变形量最大,整体叶片有向外扩张并沿切向弯曲的趋势,叶轮整体尺寸将变大。与轴配合的轮毂周围区域总变形较小,在圆形架板外边缘和四个加强板连接处变形量较大,使外缘螺孔有变形扩大的趋势。这是由于叶轮高速旋转产生的离心力以及物料和气流两相流场对其作用的缘故。
图6.8所示为负载叶轮转速为1500r/min时抛送叶轮的等效应力、等效应变及总变形云图。
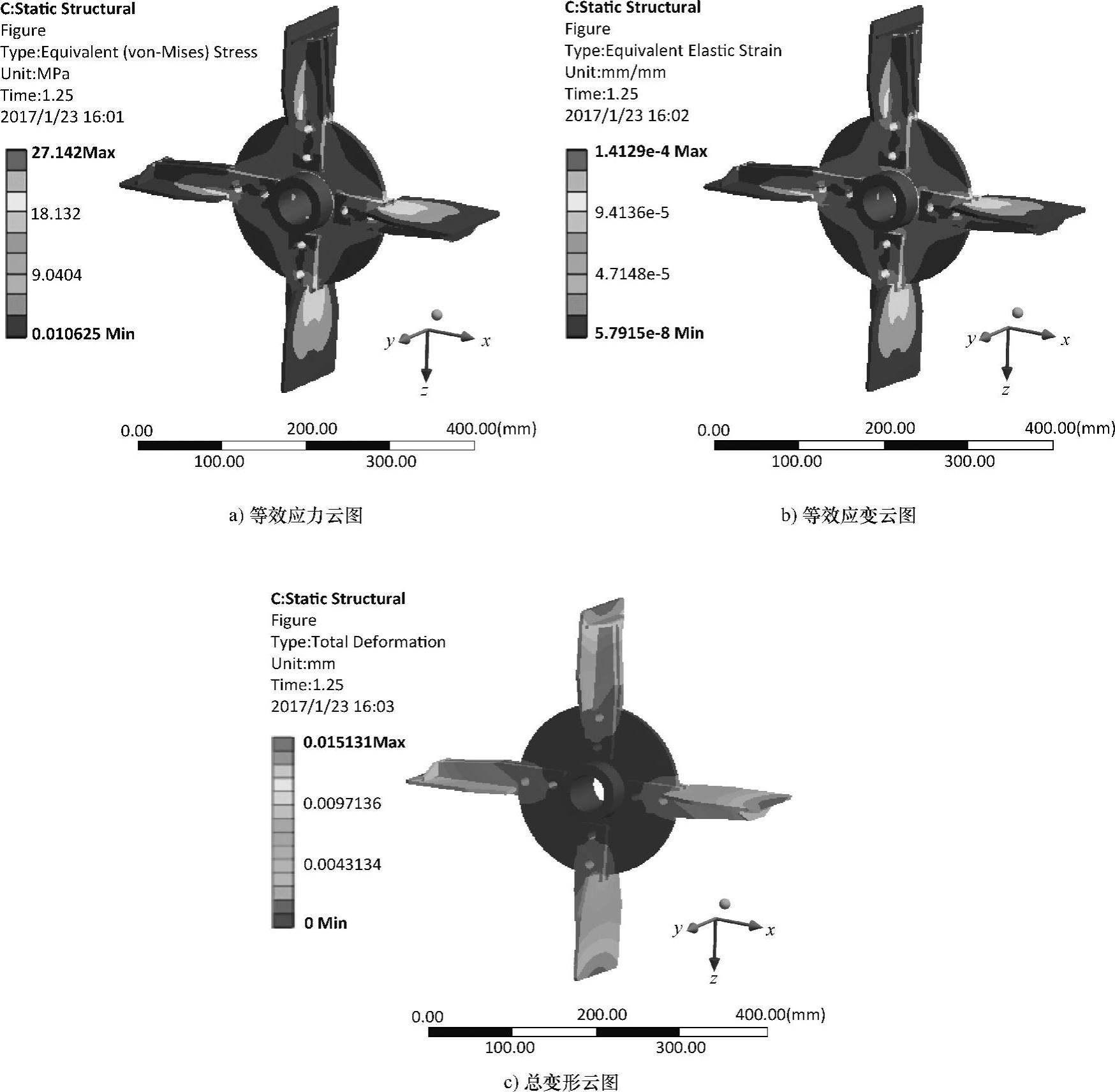
图6.8 负载叶轮转速为1500r/min时,叶轮等效应力、应变及总变形云图
由图6.8可知,负载时叶轮的等效应力、应变及总变形分布规律与空载基本相同,叶轮最大等效应力、等效应变均发生在叶片与加强板连接的边缘处靠近叶片一侧;叶片与加强板和圆形架板连接处存在明显的应力集中,且附近区域应力较大,变化较快;等效应变与等效应力的变化趋势基本相同;从总变形云图看,变形量较小,不会影响抛送装置的正常工作。
比较图6.7和图6.8可知,叶轮转速相同的情况下,负载由于抛送物料的缘故,最大等效应力(27.142MPa)、最大等效应变(1.4129×10-4mm/mm)以及最大变形量(0.015131mm)均比空载时的最大等效应力(25.435MPa)、最大等效应变(1.3225×10-4mm/mm)以及最大变形量(0.011312mm)要大,故后续分析只需分析负载情况即可。
根据静强度理论、抛送叶轮的工作条件以及叶轮选用的材料可计算出负载抛送叶轮工作时的安全系数。静强度理论式为σmax≤[σ]=σs/S,式中σmax为最大应力,σs为材料的屈服极限,σs=235MPa,故负载时安全系数S=8.66。考虑到揉碎机中抛送叶轮和揉碎锤片同轴,揉碎不同农业纤维物料时,喂入量及工作转速变化较大,叶轮承受较大的冲击载荷,同时应力集中使抛送叶轮强度降低,实际安全系数比8.66略小,故负载时静强度足够。
负载时最大变形量为0.015131mm,而抛送叶轮和外壳的径向和轴向间隙均为11mm,比较而言叶轮的最大变形量很小,不会影响抛送装置的正常工作和安全性能,刚度足够。
(2)抛送叶轮不同工况转速时的应力应变分析 与不同农业纤维物料收获及加工机械配合的叶片式抛送装置抛送叶轮转速范围一般为1500~2800r/min。对负载收获及加工不同物料的四种工况转速1500r/min、2000r/min、2500r/min以及2800r/min进行应力应变计算,求解结果如图6.9、图6.10和图6.11所示。
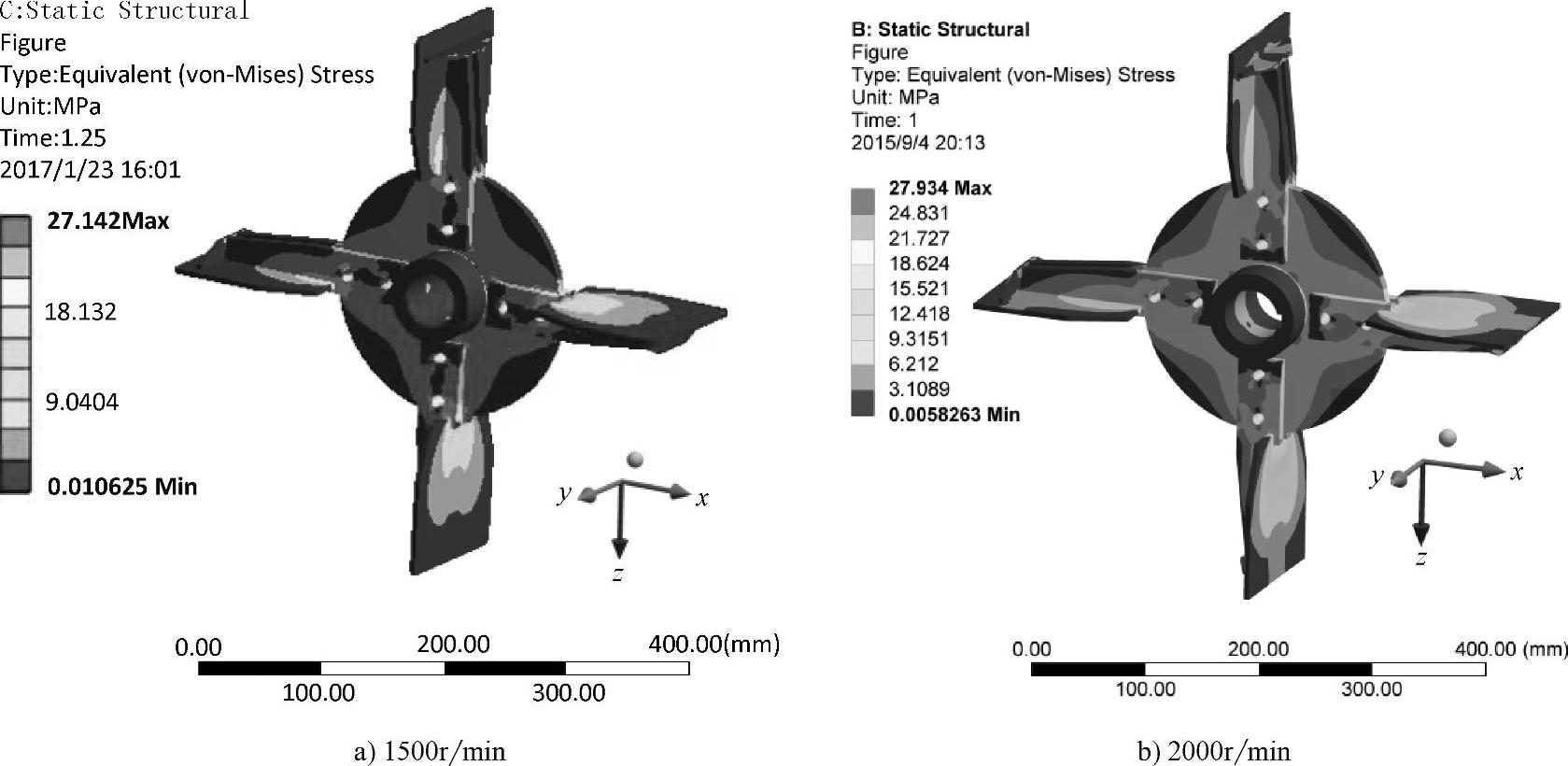
图6.9 不同转速时叶轮的等效应力云图
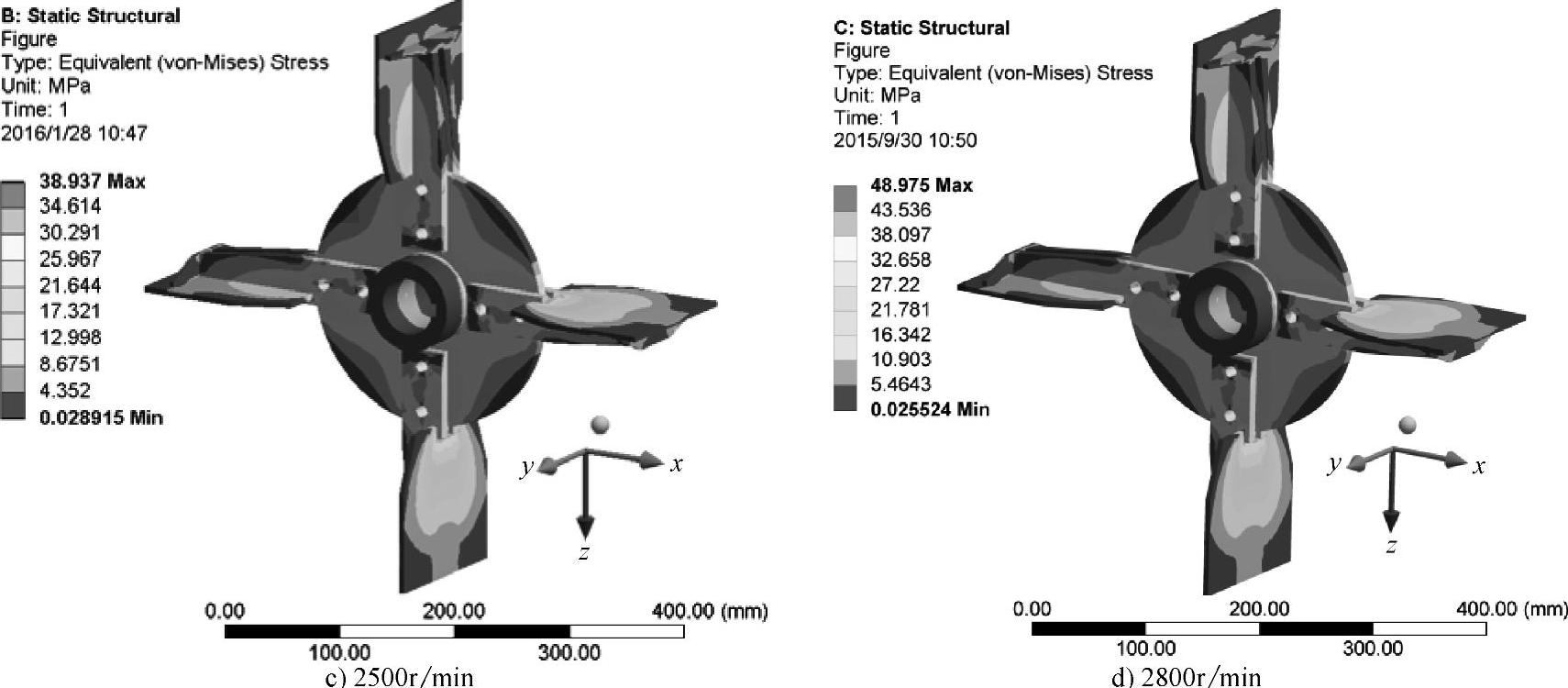
图6.9 不同转速时叶轮的等效应力云图(续)
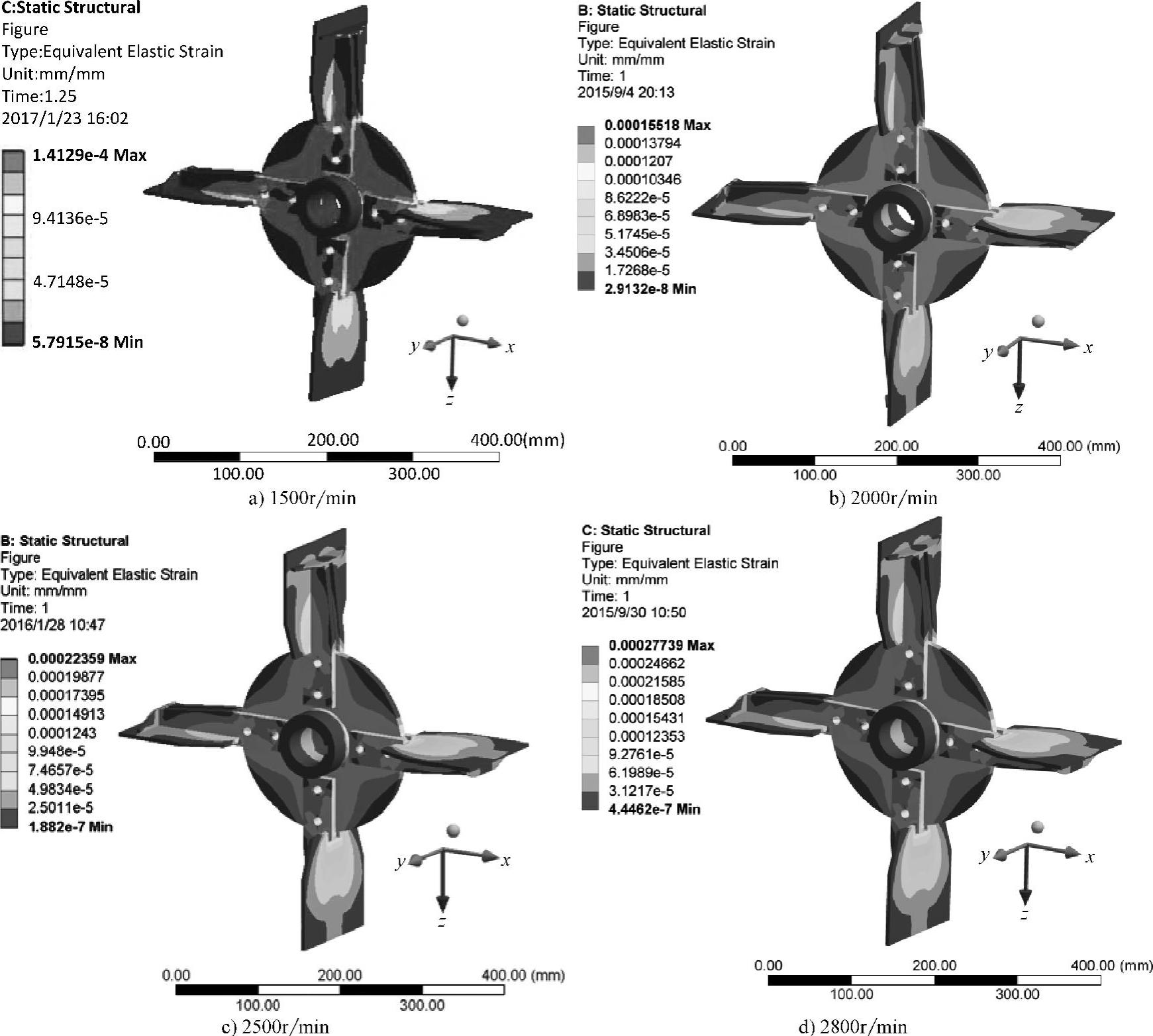
图6.10 不同转速时叶轮的等效应变云图
 (www.daowen.com)
(www.daowen.com)
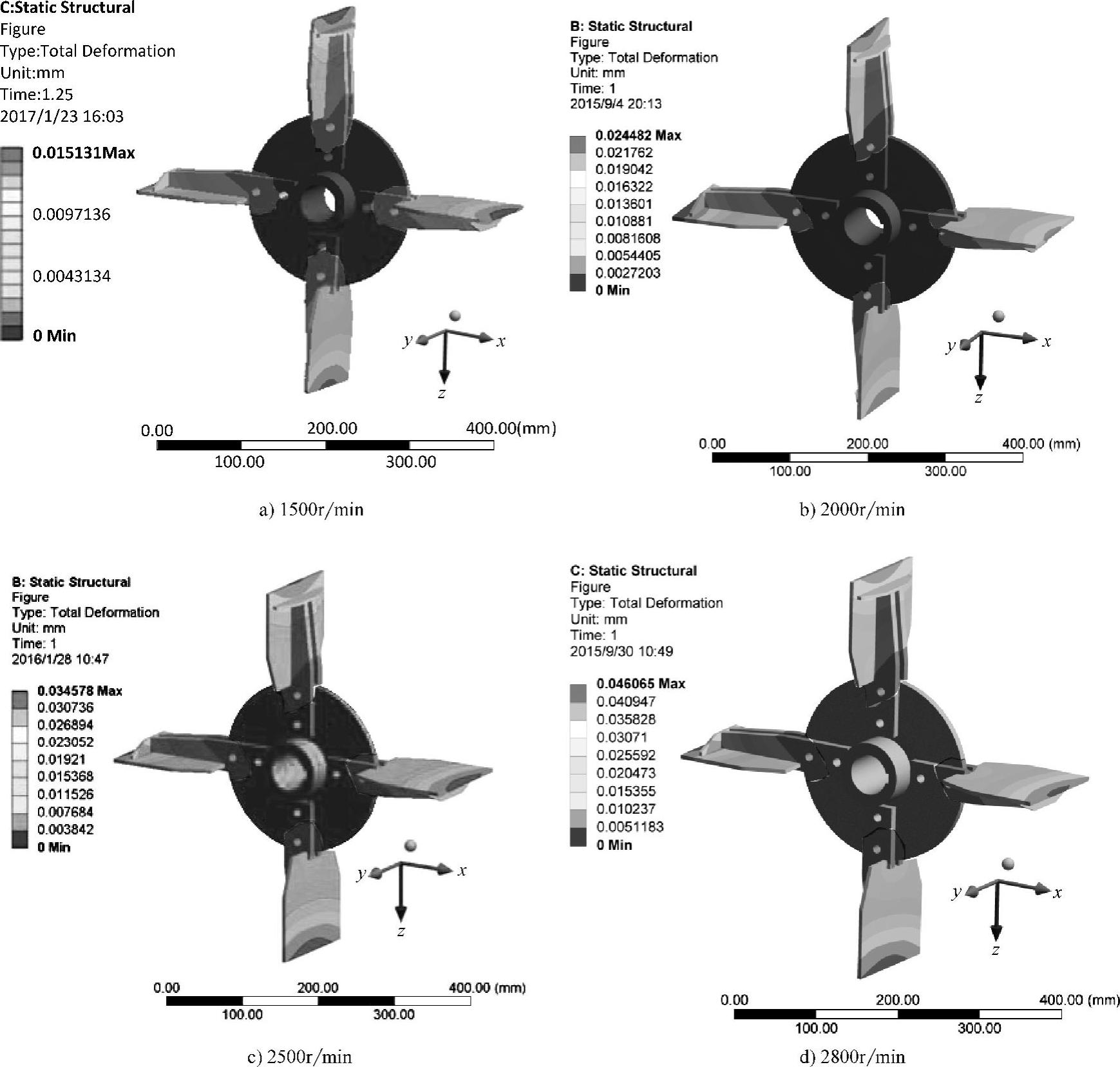
图6.11 不同转速时叶轮的总变形云图
图6.9所示为不同转速时叶轮的等效应力云图。转速为1500r/min时,最大等效应力值为27.142MPa;转速为2000r/min时,最大等效应力值为27.934MPa;转速为2500r/min时,最大等效应力值为38.937MPa;转速为2800r/min时,最大等效应力值为48.975MPa。由于叶轮转速的增大,叶轮受到的离心力随之增大,且抛送装置内物料和气流对叶轮的压力增大,所以最大等效应力随叶轮转速增加而明显增大。四种转速下,最大应力均出现在叶片与加强板和圆形架板外边缘连接处。考虑到应力集中以及叶轮承受冲击载荷,转速为1500r/min、2000r/min、2500r/min以及2800r/min时的安全系数S分别为8.66、8.41、6.03以及4.80左右,均满足静强度要求。
不同转速时叶轮的应变云图如图6.10所示,与应力分布大体一致。转速为1500r/min时,最大应变值为1.41×10-4;转速为2000r/min时,最大应变值为1.55×10-4;转速为2500r/min时,最大应变值为2.24×10-4;转速为2800r/min时,最大应变值为2.77×10-4。仿真结果表明叶轮转速越高,叶片与加强板和圆形架板外边缘连接处最大应变值越大。
图6.11所示为不同转速时叶轮的总变形云图。转速为1500r/min时,最大变形量为0.015mm;转速为2000r/min时,最大变形量为0.024mm;转速为2500r/min时,最大变形量为0.035mm;转速为2800r/min时,最大变形量为0.046mm。随着叶轮转速的增加,变形量也随之增大。四种转速下,叶轮总变形的趋势相同,从叶轮中心到叶片末端变形量逐渐增大,圆形架板区域变形量较小,变化不明显,叶片区域变形量较大,且沿叶轮径向增大趋势明显。对比叶轮与外壳的轴向和径向间隙,四种转速的叶轮整体变形量都很小,说明叶轮的刚度满足要求。
下面以叶轮转速2000r/min为例,分析叶片厚度、长度以及叶轮是否加肋对叶轮应力应变的影响。
(3)叶片厚度对应力应变的影响分析 其他工作参数不变的情况下,比较分析抛送叶轮叶片厚度对其应力、应变的影响。分别对叶片厚度为4mm、5mm和6mm的叶轮进行静力学计算,仿真结果如图6.12、图6.13和图6.14所示。
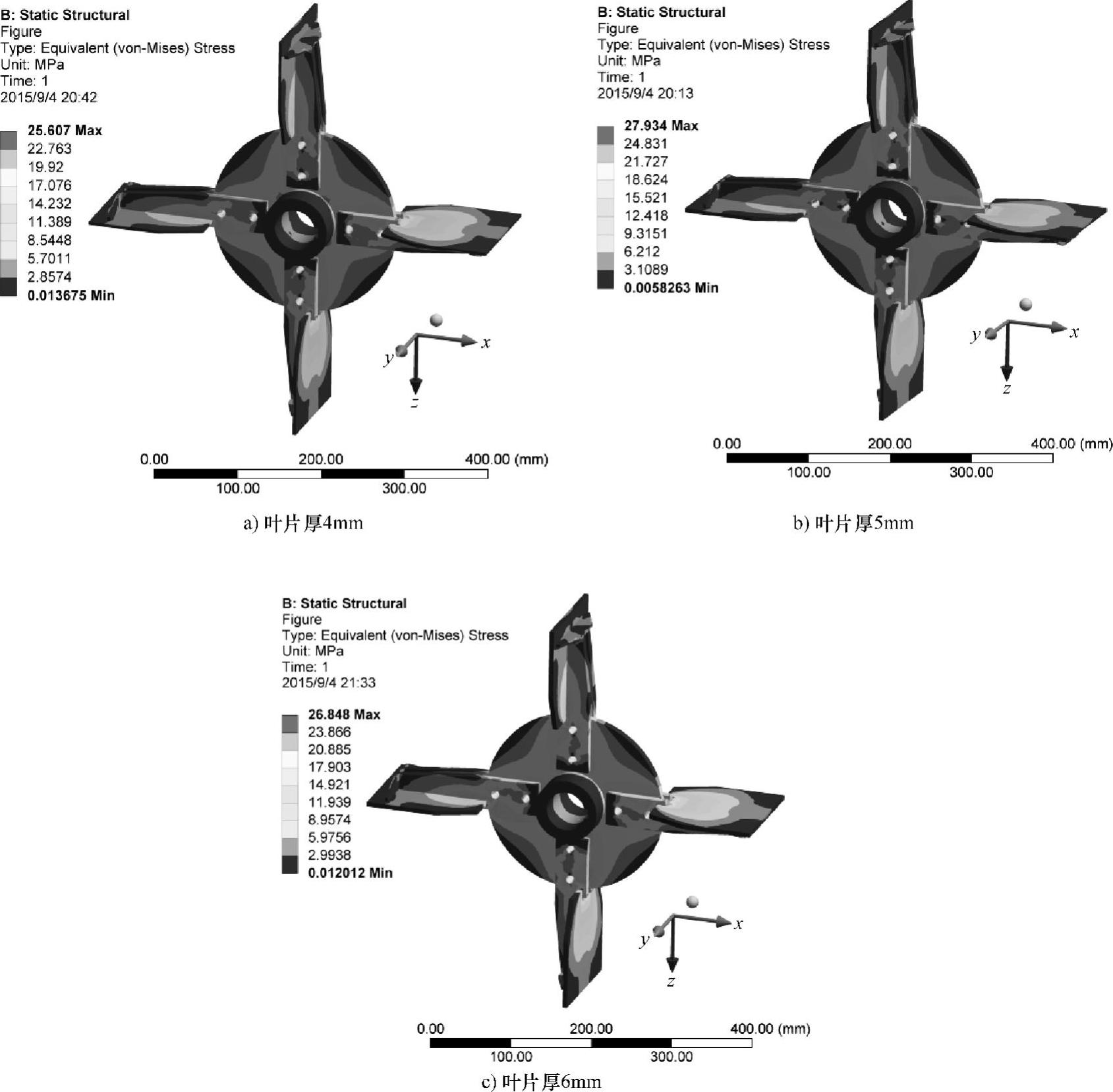
图6.12 不同叶片厚度时叶轮的等效应力云图
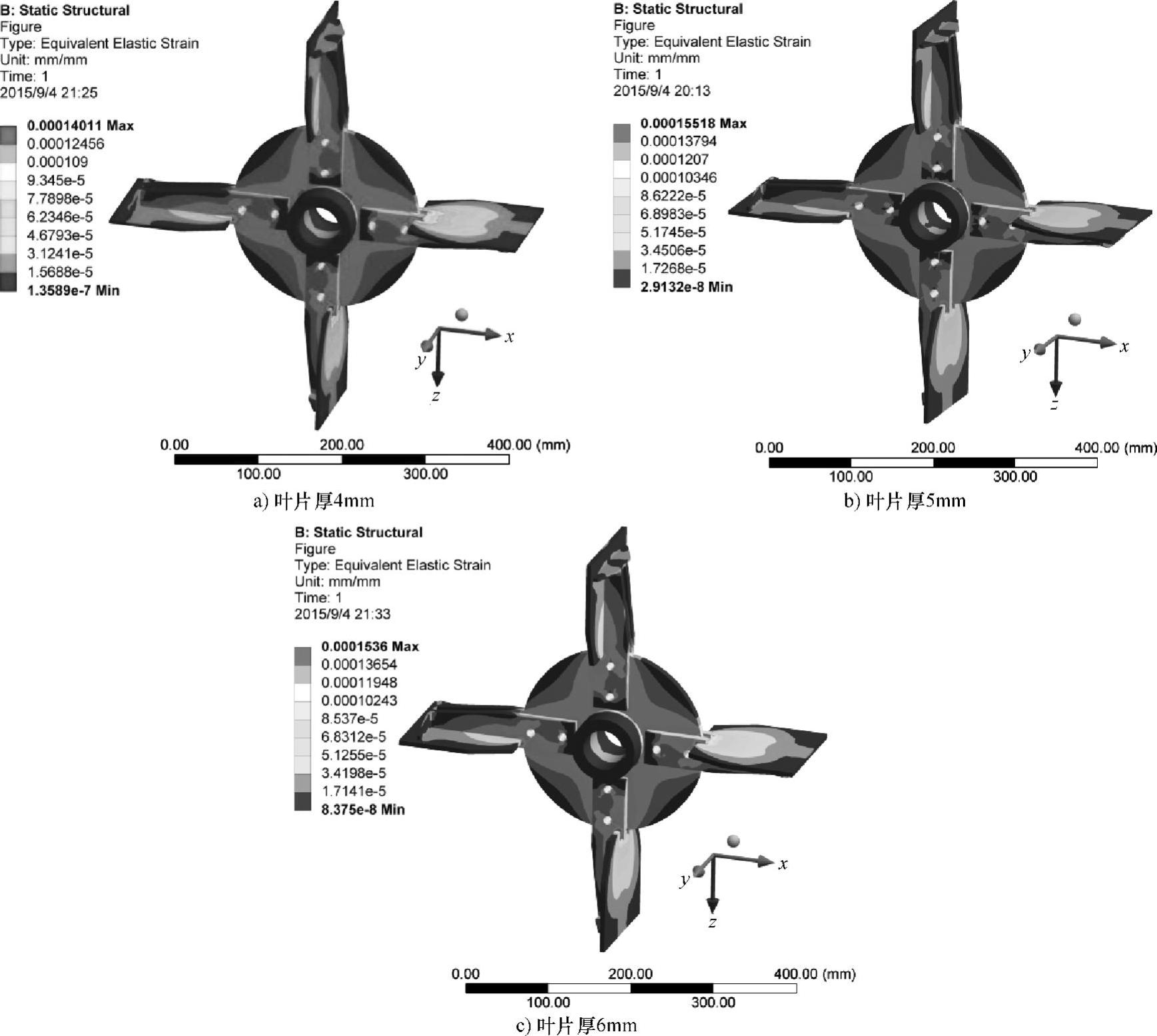
图6.13 不同叶片厚度时叶轮的等效弹性应变云图
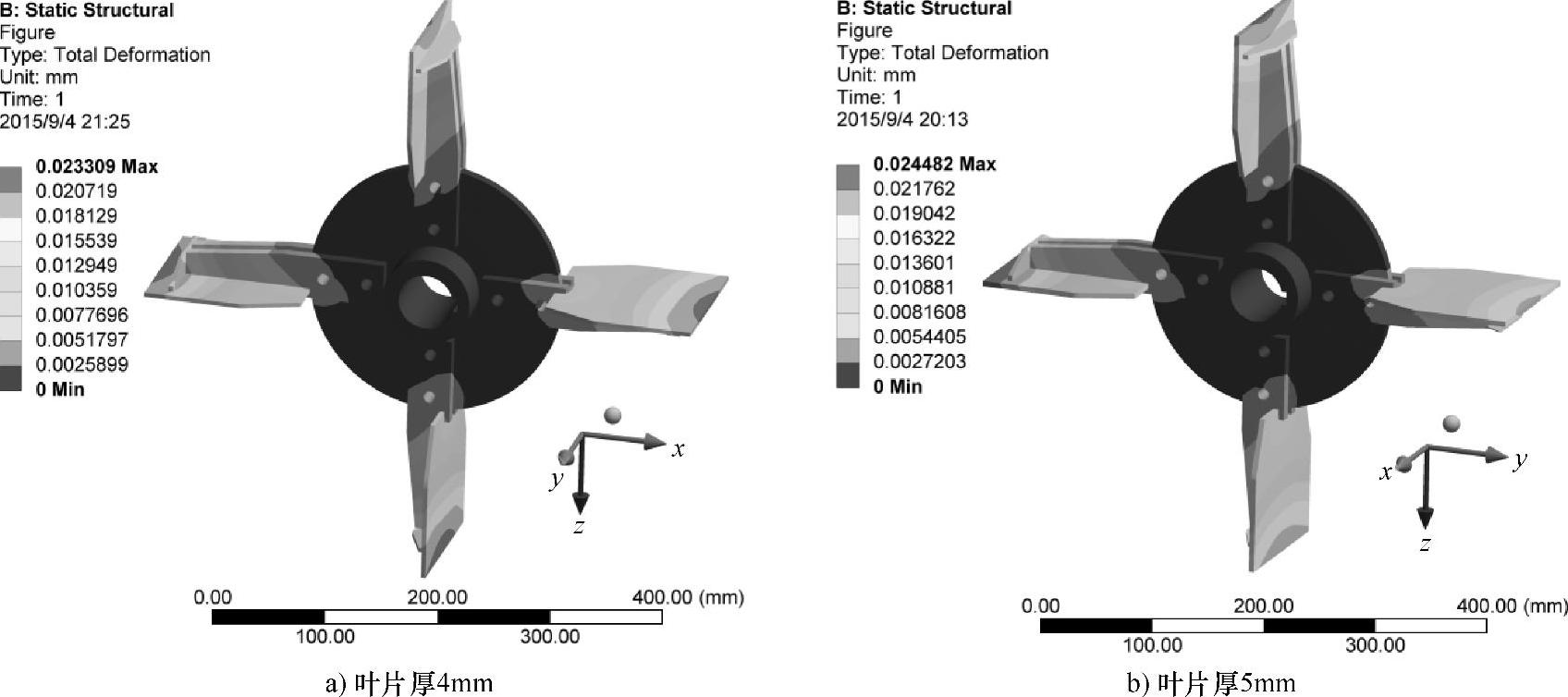
图6.14 不同叶片厚度时叶轮的总变形云图
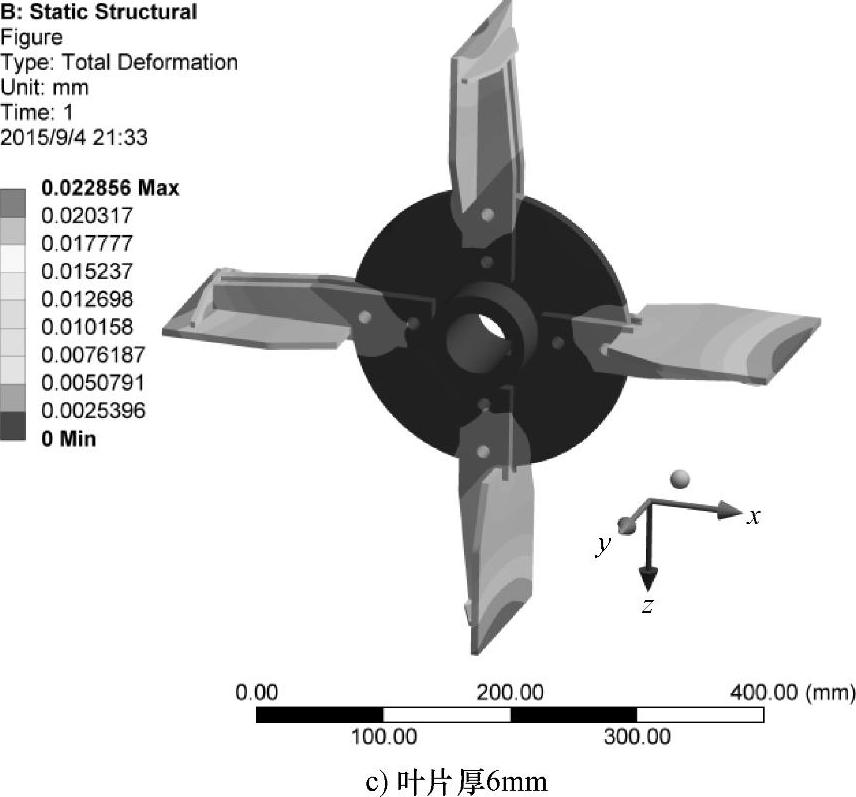
图6.14 不同叶片厚度时叶轮的总变形云图(续)
图6.12所示为不同叶片厚度时叶轮的等效应力云图。叶片厚度为4mm、5mm和6mm时,最大等效应力值分别为25.61MPa、27.93MPa和26.85MPa,应力集中部位相同。三种叶片厚度的最大等效应力接近,叶片厚5mm时应力最大,叶片厚4mm时应力最小。叶片厚度为4mm、6mm时的安全系数S分别为9.18和8.75,均满足静强度要求。可见叶片厚度对叶轮应力变化的影响不是呈正相关关系,适当地减小叶片厚度既可以降低叶轮的最大应力提高其静强度又可节省材料减轻重量。
图6.13所示为不同叶片厚度时叶轮的等效弹性应变云图。由于应力与应变关系满足胡克定律,所以应变与应力的变化趋势一致,最大应变位置同样是在叶片与加强板和圆形架板外边缘连接处。叶片厚4mm时,最大应变值为1.40×10-4;叶片厚5mm时,最大应变值为1.55×10-4;叶片厚6mm时,最大应变值为1.54×10-4。同样,三种叶片厚度的最大等效应变值非常接近,叶片厚5mm时应变最大,叶片厚4mm时应变最小。
图6.14所示为不同叶片厚度时叶轮的总变形云图。叶片厚4mm时,最大变形量为0.023mm;叶片厚5mm时,最大变形量为0.024mm;叶片厚6mm时,最大变形量为0.023mm。三种叶片厚度的最大变形都在叶片末端,最大变形量非常接近且都在许用范围之内,能够保证抛送装置安全正常地工作。
总之,抛送叶轮叶片厚度对其应力、应变及最大变形量影响不明显。适当地减小叶片厚度(叶片厚4mm)可以减小叶轮的最大应力、提高其静强度,又可节省材料减轻重量。
(4)抛送叶轮叶片长度对应力应变的影响分析 其他结构和工作参数不变的情况下,比较分析叶片长度对其应力、应变的影响。分别对叶片长度为133mm、138mm和143mm三种叶轮进行计算,仿真结果如图6.15、图6.16和图6.17所示。
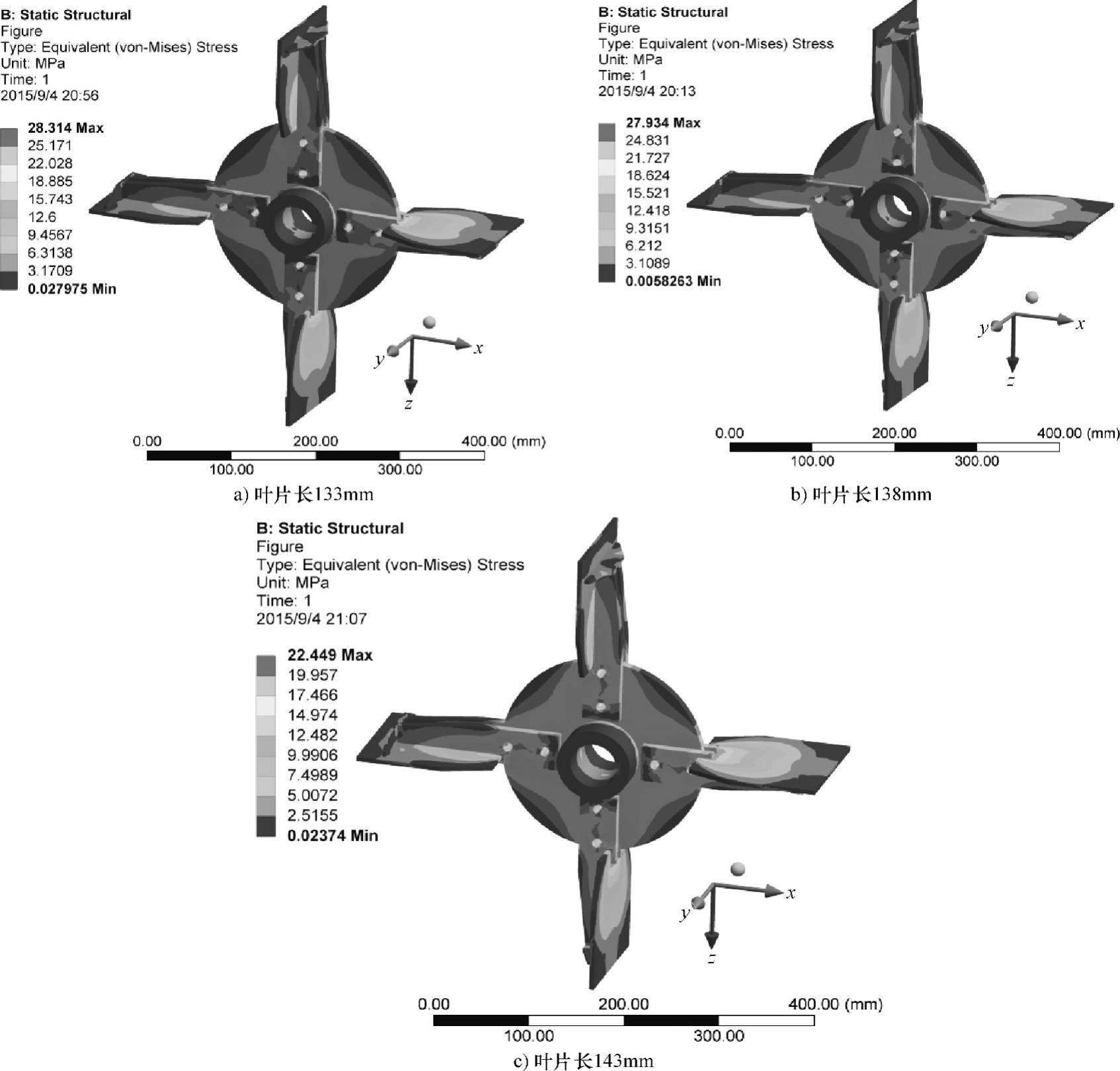
图6.15 不同叶片长度时叶轮的等效应力云图
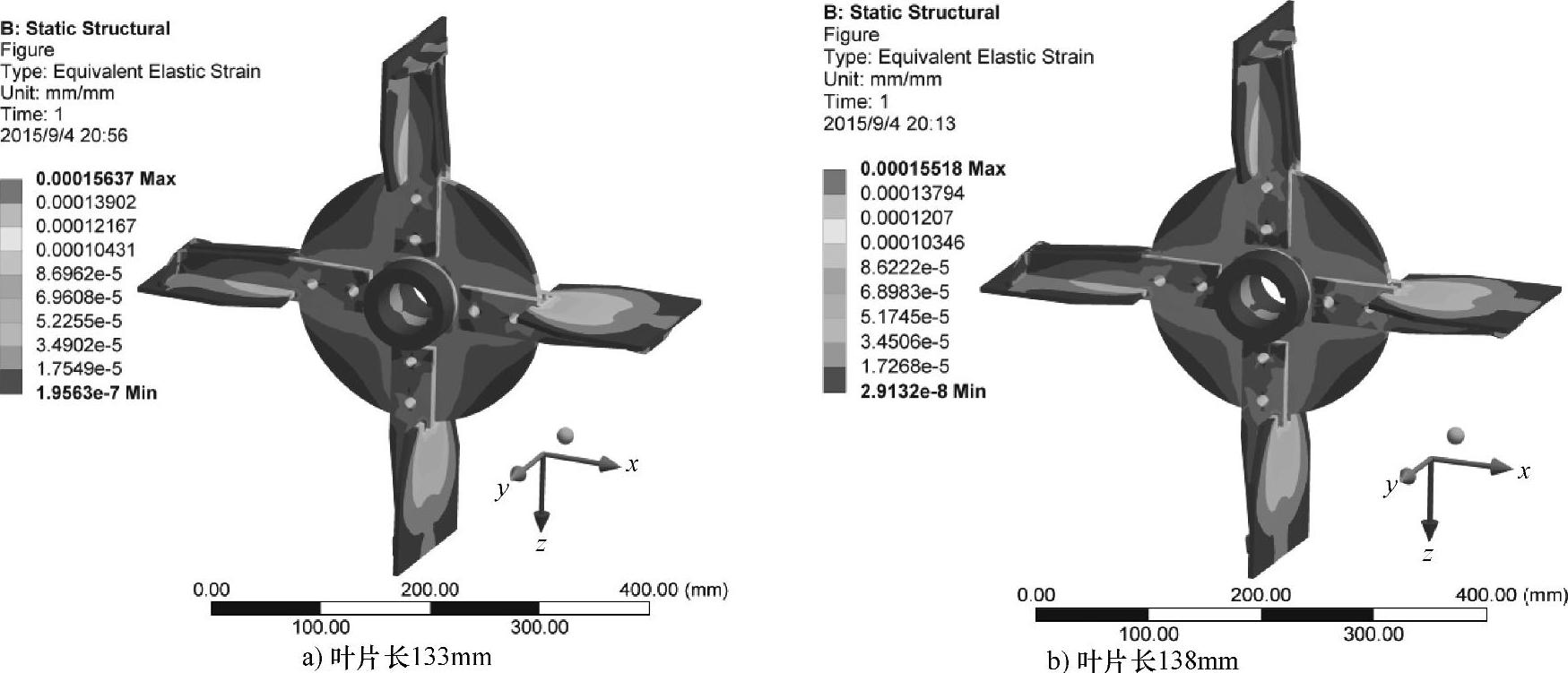
图6.16 不同叶片长度时叶轮的等效弹性应变云图
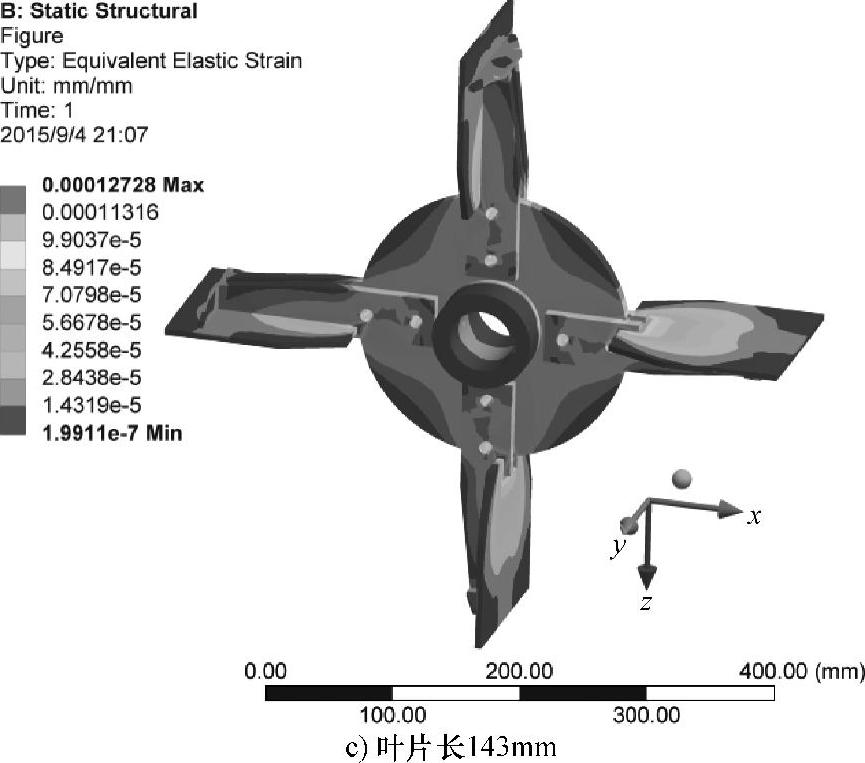
图6.16 不同叶片长度时叶轮的等效弹性应变云图(续)
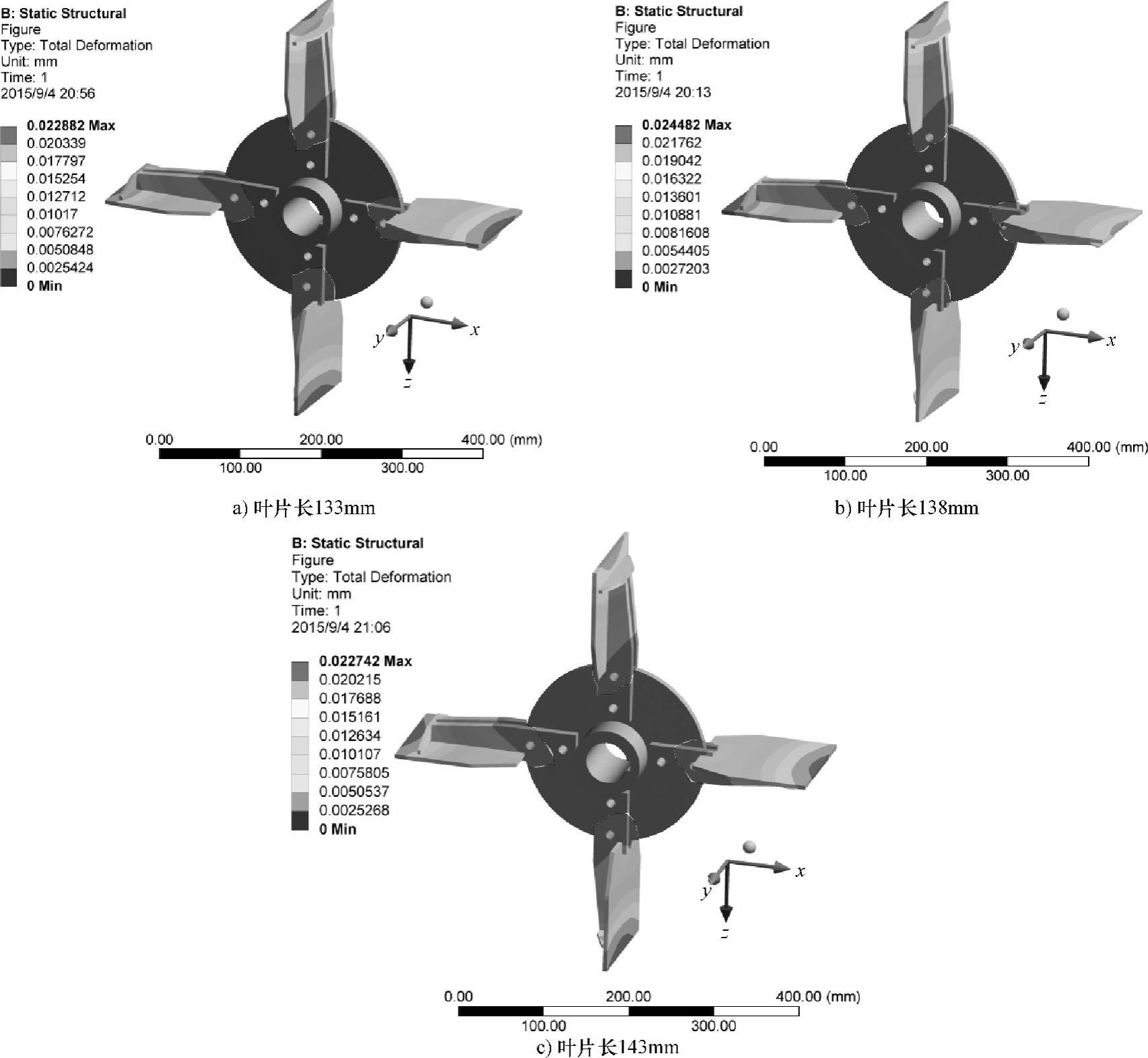
图6.17 不同叶片长度时叶轮总变形云图
图6.15所示为不同叶片长度时叶轮的等效应力云图。叶片长度为133mm、138mm和143mm时,最大等效应力值分别为28.31MPa、27.93MPa和22.45MPa,应力集中部位相同。叶片长133mm和138mm时最大等效应力接近,叶片长133mm时应力最大,叶片长143mm时应力最小。最大等效应力值随叶片长度增加而减小。叶片长度为133mm、143mm时的安全系数S分别为8.30和10.47,均满足静强度要求。
图6.16所示为不同叶片长度时叶轮的等效弹性应变云图。最大应变位置同样在叶片与加强板和圆形架板外边缘连接处。叶片长133mm时,最大应变值为1.56×10-4;叶片长138mm时,最大应变值为1.55×10-4;叶片长143mm时,最大应变值为1.27×10-4。同样,叶片长133mm和138mm时的最大等效应变接近,叶片长133mm时应变最大,叶片长143mm时应变最小。随着叶片长度的增加,最大应变值减小,与等效应力的变化趋势一致。
图6.17所示为不同叶片长度时叶轮的总变形云图。叶片长133mm时,最大变形量为0.023mm;叶片长138mm时,最大变形量为0.024mm;叶片长143mm时,最大变形量为0.023mm。三种叶片长度的最大变形都在叶片末端,最大变形量非常接近且都在许用范围之内,能够保证抛送装置安全正常地工作。
综上所述,随着叶片长度增加,叶轮最大应力及应变值均减小,而对其最大变形量影响不明显。
(5)抛送叶轮有无加强肋对应力应变的影响分析 其他结构和工作参数不变的情况下,比较分析抛送叶轮是否加加强肋对其应力、应变的影响,仿真结果如图6.18、图6.19和图6.20所示。
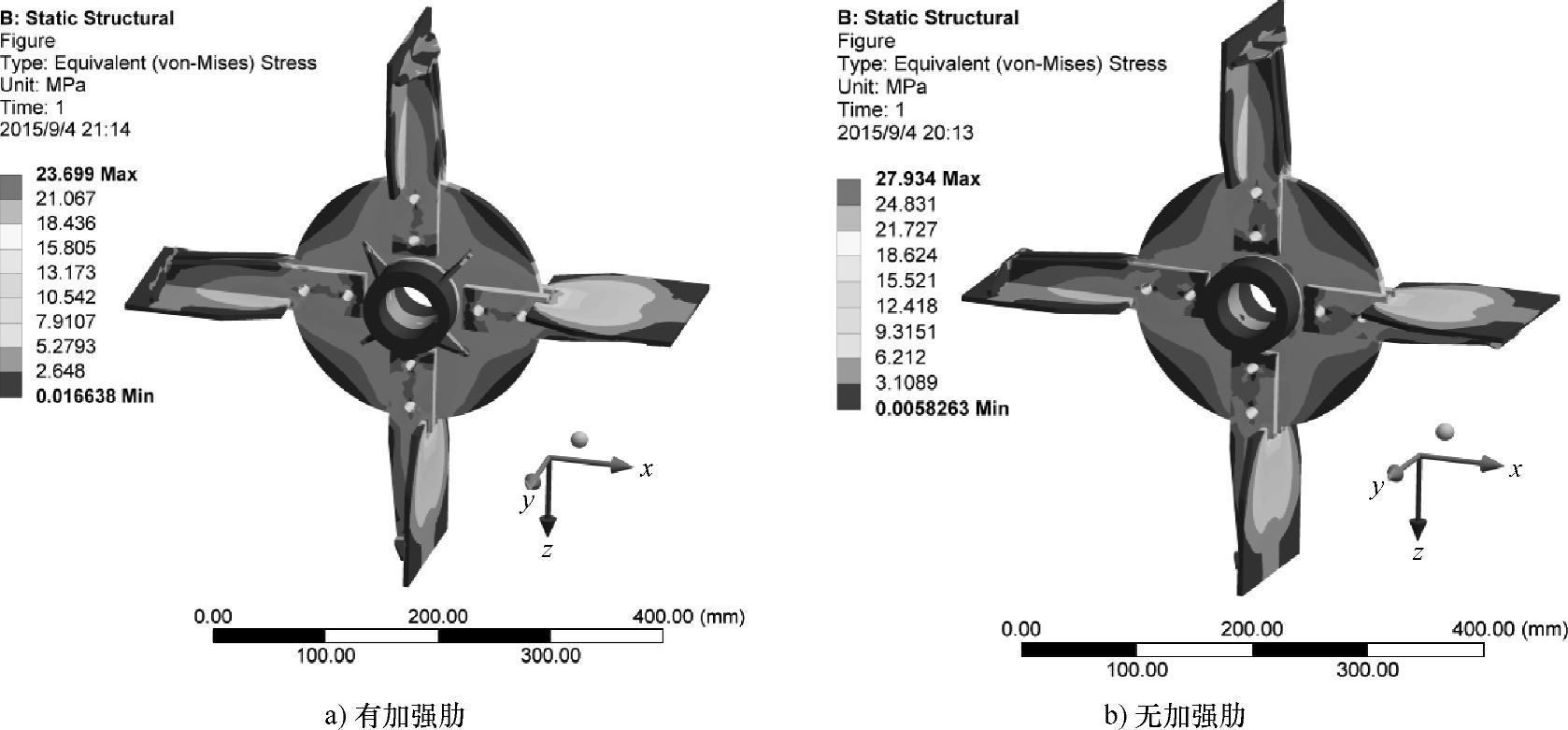
图6.18 有无加强肋结构时叶轮的等效应力云图
图6.18所示为有无加强肋结构时叶轮的等效应力分布云图。最大等效应力都出现在叶片与加强板和圆形架板外边缘连接处。在转速一定的情况下,有加强肋结构的叶轮,最大等效应力值为23.70MPa;无加强肋结构的叶轮,最大等效应力值为27.93MPa。说明加强肋结构能够减小叶轮所受的等效应力。
图6.19所示为有无加强肋结构时叶轮的等效弹性应变云图。有加强肋的叶轮最大应变值为1.36×10-4,无加强肋的叶轮最大应变值为1.55×10-4,说明加强肋结构能减小叶轮的最大应变。
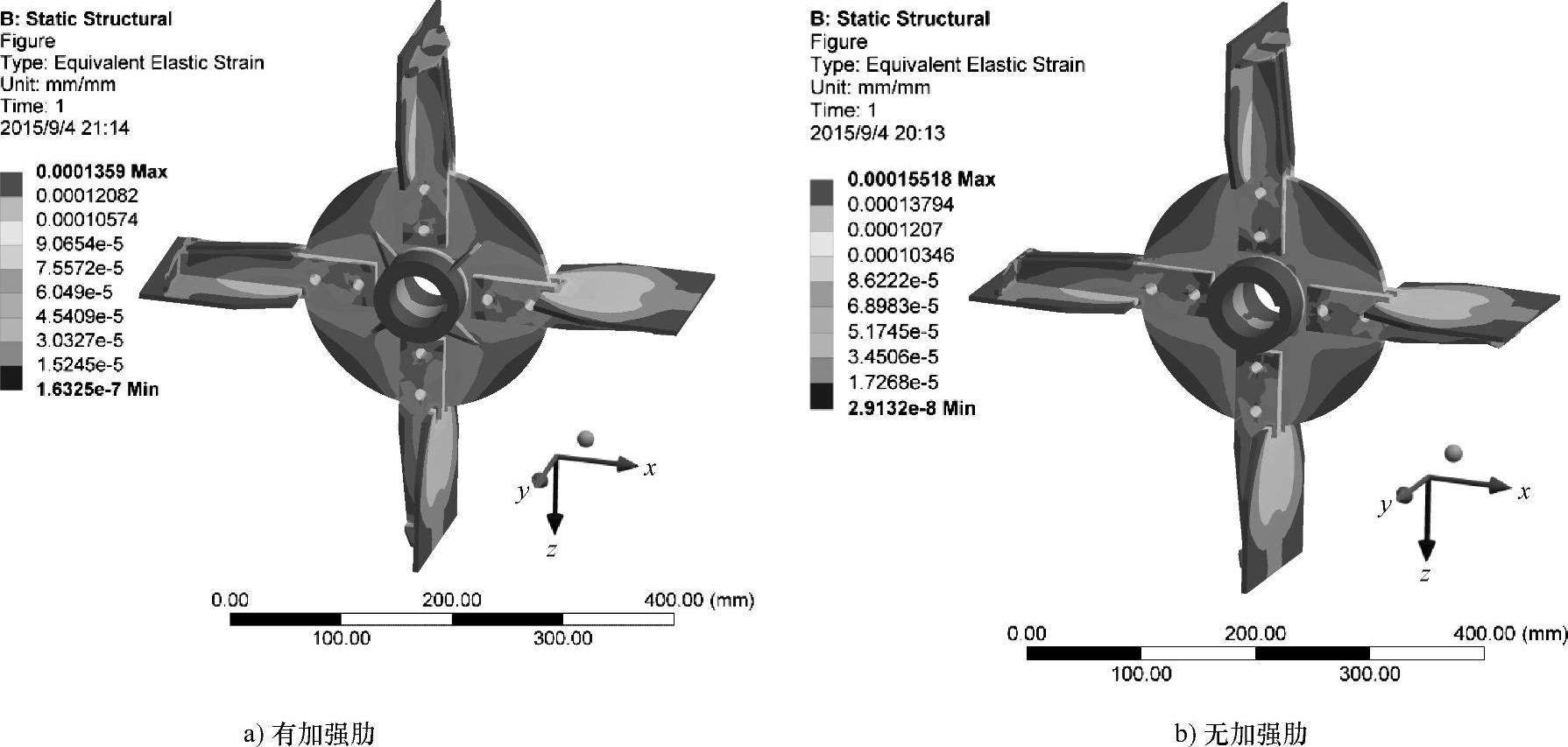
图6.19 有无加强肋结构时叶轮的等效弹性应变云图
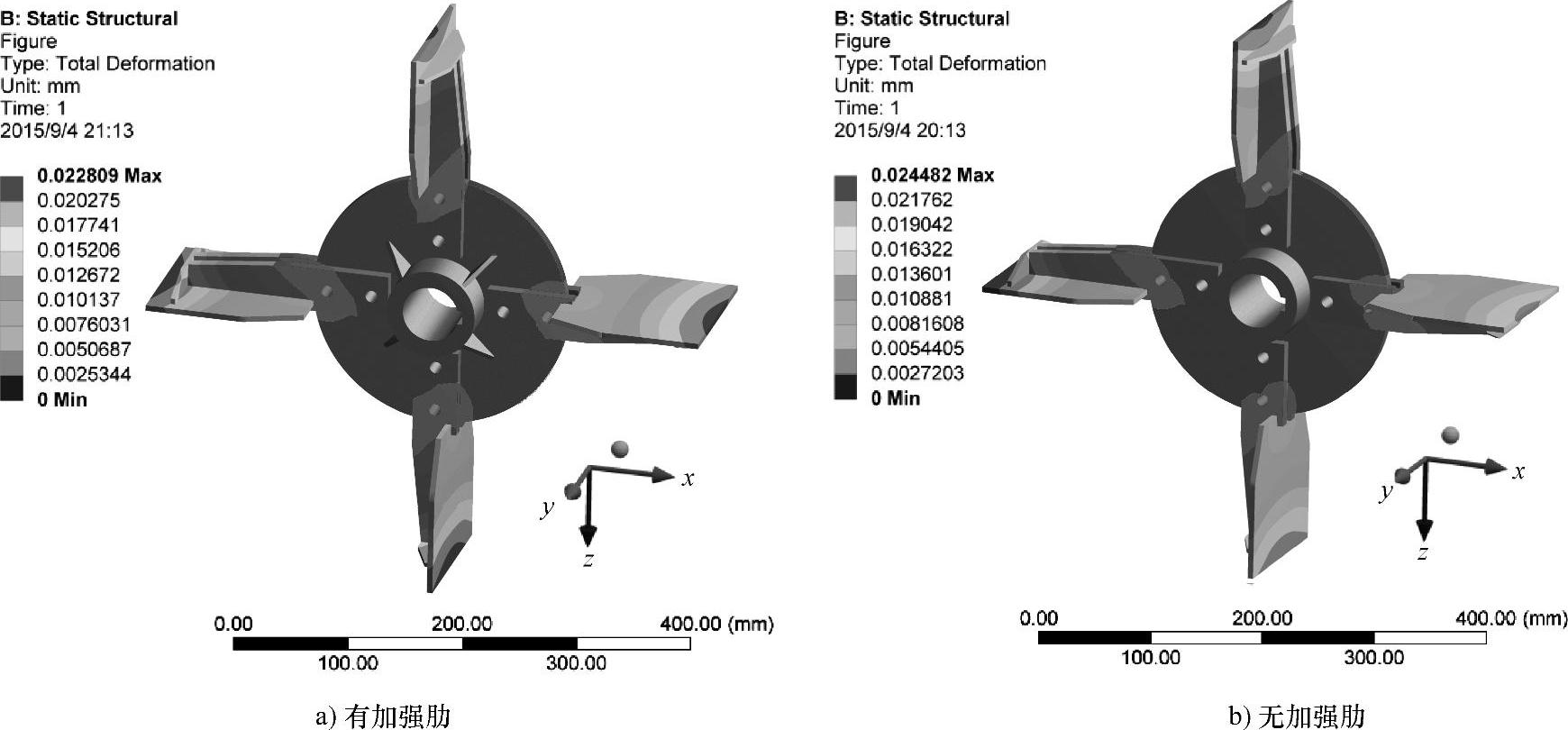
图6.20 有无加强肋结构时叶轮的总变形云图
图6.20所示为有无加强肋结构时叶轮的总变形云图。有无加强肋叶轮的变形趋势基本相同,变形量最大的位置均位于叶片的外边缘,而轮毂和圆形架板处位移变化微小。有加强肋叶轮的最大变形量为0.023mm,无加强肋叶轮的最大变形量为0.024mm,说明加强肋结构能够减小叶轮工作时的变形量,但减小量不大。
可见,加强肋结构能够使叶轮的等效应力、应变及总变形都减小。
综上所述,叶轮的转速对叶轮应力、应变及总变形影响最大;叶片长度以及叶轮是否有加强肋对叶轮应力、应变的影响次之,对总变形影响不大;而叶片厚度对叶轮应力、应变及总变形的影响均较小。
4.叶片监测点应力值变化规律分析
由应力云图可知,在叶片与加强肋和圆形架板连接处存在最大应力,故在此区域内设定监测点且与试验点位置相同。图6.21所示为空载叶轮转速为1500r/min且运行稳定后监测点在0.25s内不同时刻所受应力的仿真计算结果。
由图6.21可以看出,监测点应力值呈准周期性变化,应力变化周期即为叶轮旋转周期,最大应力值为8.75MPa,最小应力值为4.72MPa,平均应力值为6.735MPa。负载以及空载叶轮转速为其他值时,监测点应力值变化规律与此应力变化规律类似,只是应力最大值、最小值、平均应力值以及变化周期与此工况的值不同。
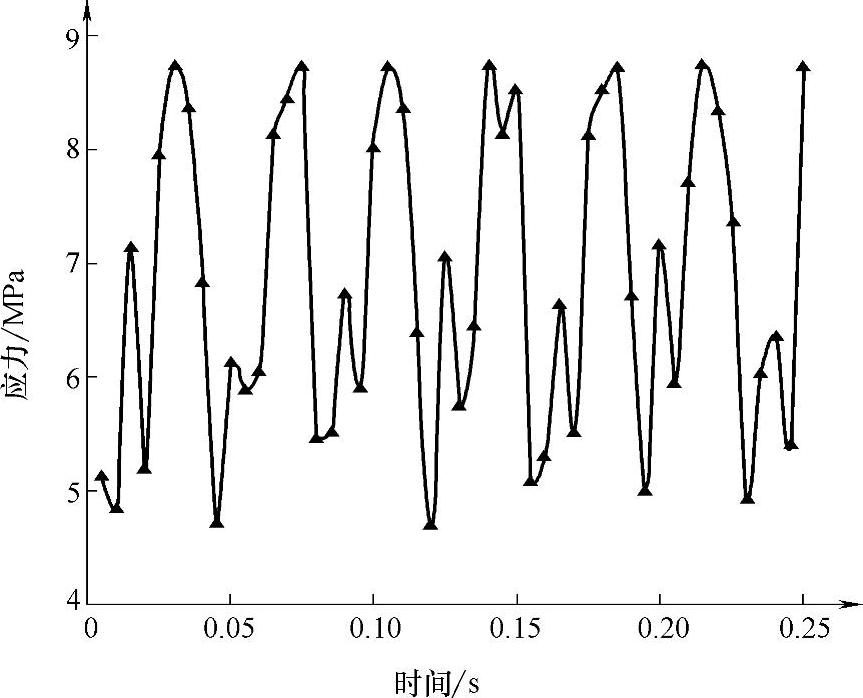
图6.21 0.25s内监测点应力仿真值
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








