数值建模所采用的尺寸均为叶片式抛送装置试验台的实际尺寸，本章中试验台抛送装置尺寸调整为与9R-40型秸秆揉碎机中的抛送装置相同。叶轮外径为ϕ500mm、叶片宽度为160mm、叶片厚5mm，叶片为径向4叶片；圆形外壳内径为ϕ522mm，出料管横截面为166mm×166mm的方形，直管高度为500mm，弯管外圆弧半径为998mm，叶片式抛送装置试验台如图1.3所示。所抛送物料为黄玉米秸秆切碎段，切碎长度为10～15mm、平均直径为ϕ13.5mm，当量直径为7.53mm，平均密度为90.9kg/m³。叶轮转速以1500r/min为例进行计算。

计算区域、网格划分以及边界条件等同4.3节基于Eulerian模型的气固两相流数值模拟。由于抛送装置具体参数值不同，整个装置流道区域共划分为1289165个网格，节点数为286911。

1.叶片式抛送装置内气流场数值计算

对叶片式抛送装置内的气流场进行数值模拟时，先对其进行稳态流场计算，当稳态流场收敛后再进行非稳态流场计算。在抛送装置实际工况下，随着叶轮转动，叶轮所处区域流场也随时间变化而变化，先进行稳态流场计算，确定参数选择的正确性后再进行非稳态流场计算，能有效缩短非稳态流场的计算时间，且使非稳态流场数值模拟更接近真实流场。计算稳态流场时选用有限体积法离散控制方程，湍流模型选用标准k-ε模型，控制方程采用分离式隐式方法求解，离散格式采用一阶迎风格式，数值计算选用SIMPLE算法。当叶轮旋转过程中气流流动稳定后，对叶片式抛送装置内气流场做非稳态计算，模型选用RNGk-ε湍流模型，数值计算选用SIMPLEC算法，以加快非稳态的收敛速度。离散格式选用二阶迎风格式计算，以提高流场计算精度。设置时间步长为0.0001s，迭代步数为400步，每步迭代30次，设置收敛标准为稳态监测项残差均小于1×10^-3，非稳态监测项残差均小于1×10^-2，且各项输出保持平稳。本次迭代133次稳态结果收敛；继续进行非稳态计算，计算4000步后非稳态计算迭代残差图如图6.1a所示。残差图波动稳定且规律，同时非稳态计算出口流量波动较小且稳定，具有周期性，故迭代计算收敛。

2.叶片式抛送装置内气固两相流场数值计算

抛送装置内气固两相流数值计算与气流流场数值计算步骤基本相同，先进行稳态气固两相流场计算，当稳态流场收敛后再进行非稳态气固两相流场计算。选取Eulerian模型进行气固两相流模拟计算，稳态数值计算方法同4.3节基于Eulerian模型的气固两相流数值模拟。稳态计算收敛后对叶片式抛送装置内气固两相流场做非稳态计算，选用RNGk-ε湍流模型，计算方法选用Phase Coupled SIMPLE，控制方程及迎风格式与单相非稳态流场计算相同。气固两相稳态流场迭代192步收敛；继续进行非稳态计算，经4000步后非稳态计算结果收敛，迭代残差图如图6.1b所示。

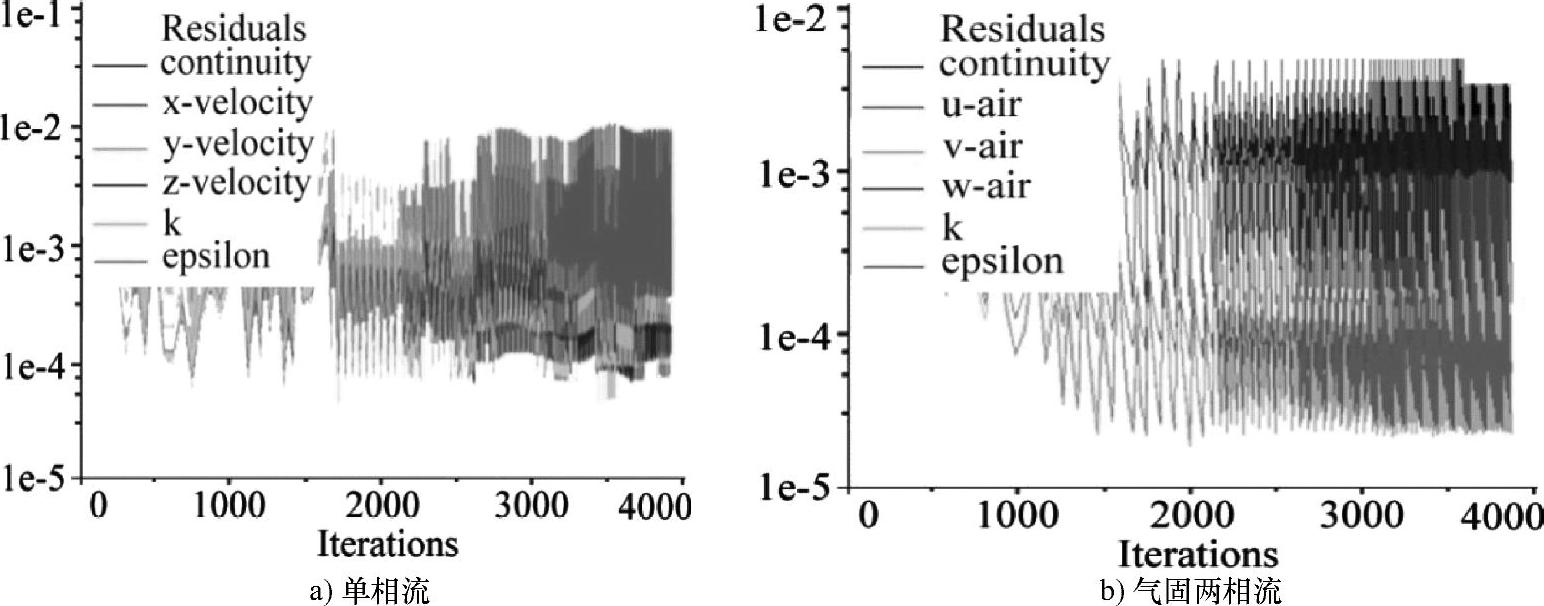
图6.1 流场数值计算迭代残差图

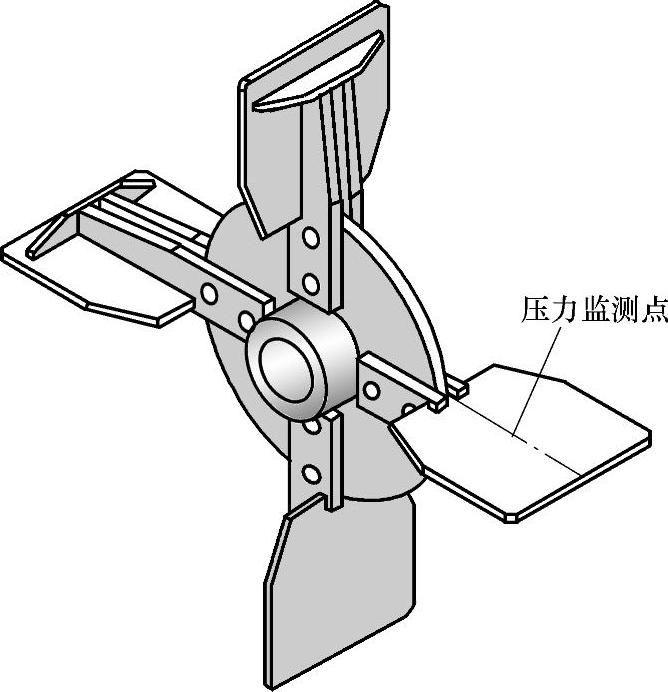
图6.2 叶轮压力监测点位置

3.流场压力载荷输出(www.daowen.com)

单向流固耦合过程中，直接将流场数值计算结果中叶轮表面压力载荷输出并加载到叶轮结构耦合面上。此处的流场压力载荷是指分布在叶轮表面的一类力，它作用在叶轮的每个表面，由于抛送装置内流场在实际运动过程中是不均匀的，所以流场压力载荷的分布也是不均等的。本文用于分析的叶轮压力载荷由Fluent的“.inp”文件导出，已将整个叶轮受到的流场载荷转化为分布在叶轮结点处的压力和集中力。

以图6.2所示的叶片表面监测点所受载荷为例输出流场压力载荷。监测点数据能够直接反映叶片在不同时刻所受流场压力值大小。

监测点选定后设置输出形式，输出选定为最大总压输出，设置输出横坐标为时间，非稳态气流流场中监测点输出总压力如图6.3所示。

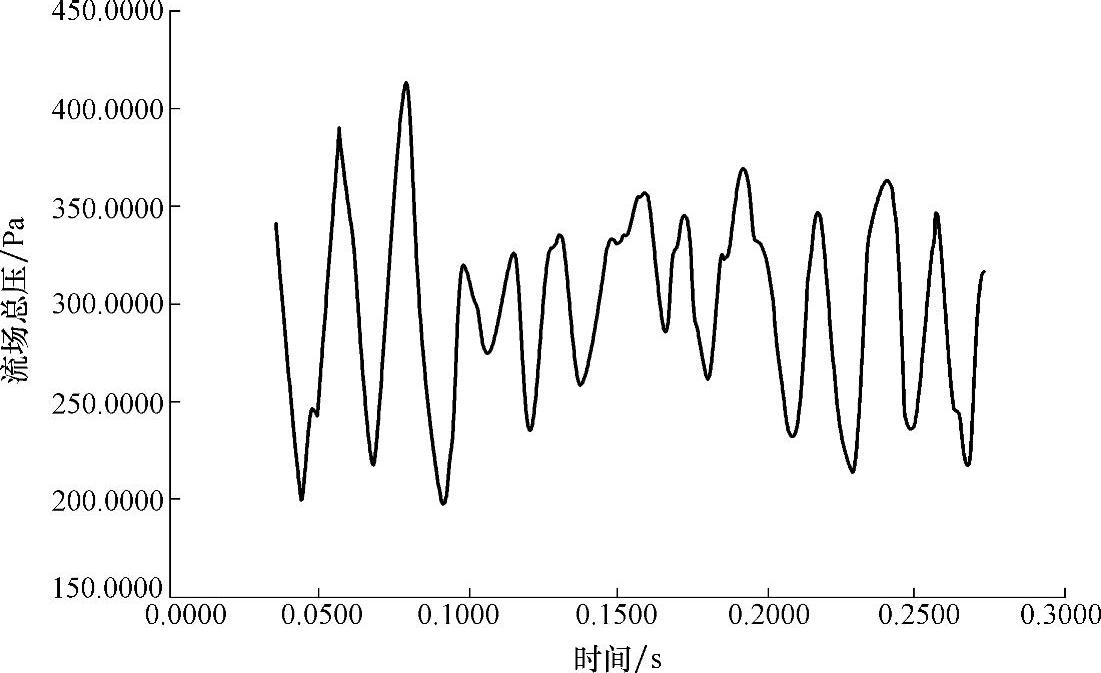
图6.3 非稳态气流流场中监测点输出总压力

由图6.3可知，数据开始记录时由于非稳态流场没有达到收敛状态，流场内气流尚不稳定。当流场收敛稳定后，叶片所受压力成准周期性变化，叶轮所受压力大小在每个周期内会出现小范围波动。这是由于叶轮在旋转一周的过程中临近进料口处气体压力会增大，旋转至出料口时，由于气体的回流作用，形成低压区，使得流体对叶轮压力降低的缘故。

非稳态气固两相流场中监测点输出总压力如图6.4所示。

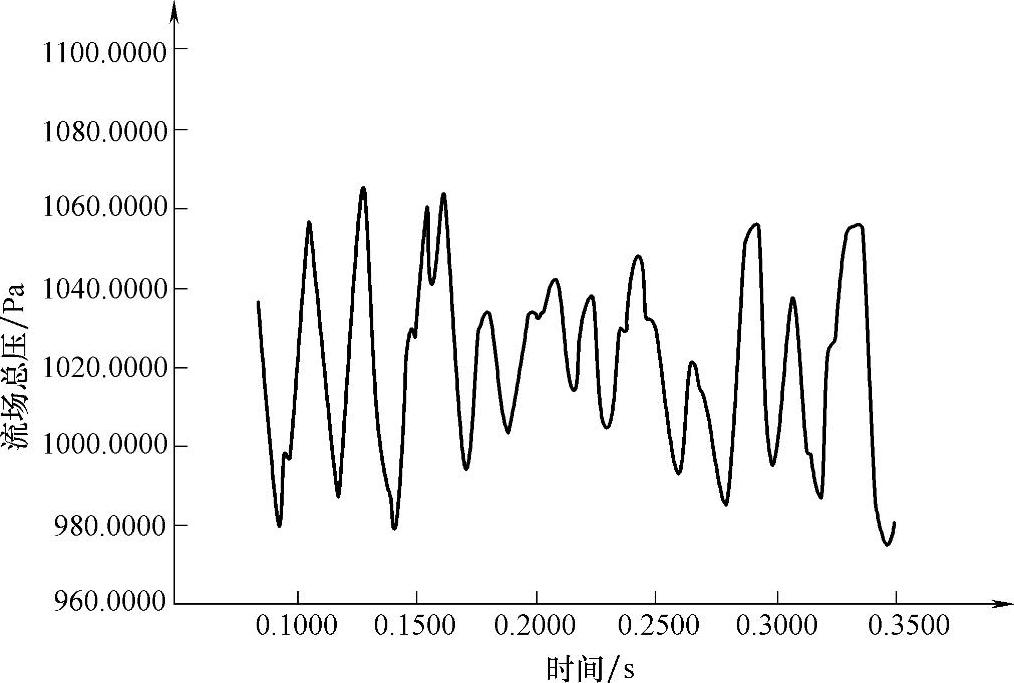
图6.4 非稳态气固两相流场中监测点输出总压力

由图6.4可知气固两相流场稳定后叶轮所受压力仍然呈准周期性变化，与气流场压力值相比，由于流场中增加物料对叶轮的作用，使得气固两相流场对叶轮的压力大于气流场对叶轮的压力。