（1）数学模型 叶片式抛送装置抛送青（黄）玉米秸秆切碎段时，所抛送物料颗粒尺寸较大，斯托克斯数大于1，物料颗粒独立于流场运动，且由于物料的体积分数大于10%，抛送物料时相间有较强的耦合，同时考虑到计算精度，选取欧拉-欧拉方法中的Eulerian模型模拟。叶片式抛送装置工作时温度变化不大，不考虑两相间的能量交换，控制方程为质量守恒和动量守恒方程。Eulerian模型第k（分别表示气流相a和物料颗粒相p）相的连续方程为

式中 ρ_k——第k相的密度（kg·m³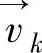）；——第k相的速度（m·s^-1）；

α_k——第k相的体积分数；

t——时间（s）。

Eulerian模型气流相（即a）的动量守恒方程为

式中 p——所有相共享的压力（N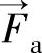）；——外部体积力（N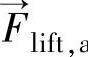）；——升力（N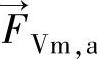）；——虚拟质量力（N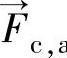）；——哥氏力（N）；

K_ka——相间动量交换系数，且K_ka=K_ak；

n——相的总数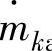；——相间传递的质量（kg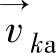）；——相间的速度（m/s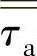）；——气流相的压力应变张量。

物料颗粒相（即p）的动量守恒方程为

式中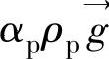——物料颗粒重力（N），其余参数含义同上，只是下标为p表示物料颗粒相应参数。

式（4.7）、式（4.8）中，第k相的压力应变张量为

式中 μ_k和λ_k——k相的剪切和体积黏度。

主相a中作用于第二相p的升力为

且F_lift，a=-Flift，p(www.daowen.com)

主相a对第二相物料颗粒p施加的虚拟质量力为

且F_Vm，a=-F_Vm，p

哥氏力为

式中 ω——叶轮的角速度（rad/s）；

r——叶片的向径（m）。

抛送叶轮围绕z轴旋转的角速度为ω，在笛卡儿坐标系下，哥氏力在x和y轴方向的分力为

式中 u_y，p、u_y，a——颗粒与气流在y轴方向的速度（m/s）。

式中 u_x，p、u_x，a——颗粒与气流在x轴方向的速度（m/s）。

抛送叶轮的高速回转使得流场处于湍流状态，选择标准k-ε两方程湍流模型使方程封闭。

（2）计算区域和网格生成 叶片式抛送装置试验台上调整具体参数同4.2节，计算区域的实体模型的建立及网格划分同4.2.1节网格生成。所抛送物料为青（黄）玉米秸秆切碎段，切碎长度为10～15mm、平均直径ϕ13.5mm，当量直径为7.53mm，平均密度为90.9kg/m³，进料口处物料体积分数为0.2，进料速度为6.5m/s；叶轮转速为650r/min。

（3）数值模拟计算方法和边界条件设定 叶片式抛送装置工作时其内气固两相流动采用Fluent软件提供的Eulerian多相流模型，其余同4.2.1节数值计算方法。

边界条件除物料粒径为7.53mm，密度90.9kg/m³外，其余同4.2.1节中的边界条件设置。