1.数学模型

对于模拟多相混合的流场，当存在大范围的颗粒相分布或者界面规律未知或者它们的可靠性有疑问时，较适合选用经过简化的Mixture模型，它适用于模拟从稀疏到中等密度复杂的两相流或多相流。Mixture模型需求解的方程少，计算稳定性好，当求解变量的个数小于完善的多项流模型时，能和完善的多项流模型一样取得好的结果。该模型的相间耦合是很强的，因此可应用于叶片式抛送装置抛送小麦秸秆粉碎颗粒时内气固两相流动数值计算。

混合模型的连续性方程为[45]

其中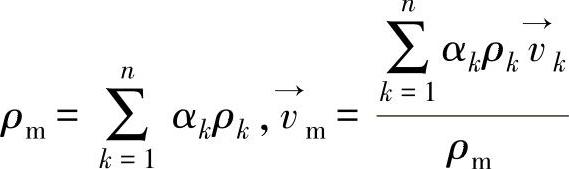

式中 ρ_m——混合密度（kg/m³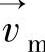）；——质量平均速度（m/s）；

n——相数；

α_k——第k相的体积分数；

ρk——第k相的密度（kg/m³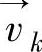）；——第k相的速度（m/s）。

混合模型的动量方程为

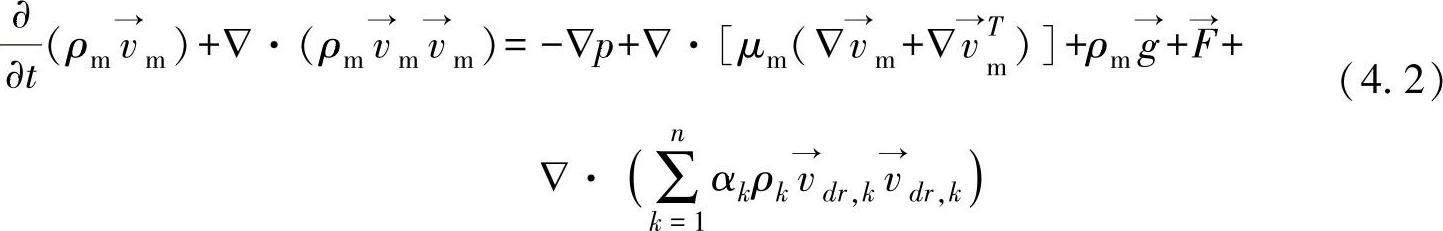
式中 μ_m——混合黏性系数（Pa·s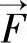）；——体积力（N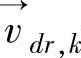）；——第k相的飘移速度（m/s）。

其中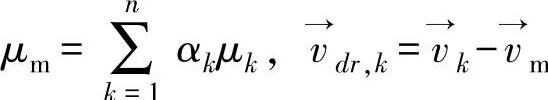

相对（滑流）速度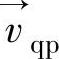为第二相（p）相对于主相（q）的速度

飘移速度和相对（滑流）速度的关系为

第二相的体积分数方程为(www.daowen.com)

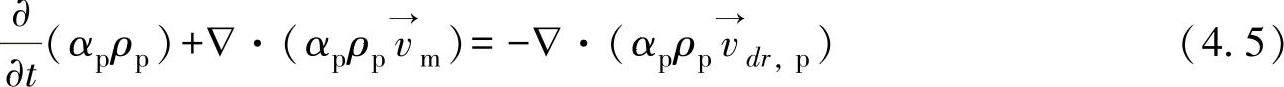
2.基本假设

叶片式抛送装置工作时，其内部流动是三维非稳态可压缩的气固两相流动，且存在着叶轮和壳体的动静干涉问题以及气流和物料的相互影响，使得流动非常复杂。在对叶片式抛送装置的内部流动进行数值模拟时需做如下假设：

1）叶片式抛送装置通常在常温下工作，因此不考虑气固两相之间的能量交换；设气相为不可压缩流体；颗粒相也为连续介质，且每相的物理特性均为常数。

2）颗粒相为球形、粒径均匀的物料颗粒，且不考虑相变。

3）采用多重参考系模型（Moving Reference Frames，MRF）作为定常流动来近似模拟这个非定常流场。

3.计算区域和网格生成

叶片式抛送装置试验台上调整具体参数为叶轮外径700mm、叶片宽度160mm、叶片厚5mm，叶片数为4，径向叶片，叶轮转速为650r/min。所抛送物料为小麦秸秆粉碎颗粒，平均粒径为0.5mm，密度为75.9kg/m³；进料口处物料体积分数为0.2。

选取叶片式抛送装置的流动空间作为计算区域（图4.1a）。物料和气流从进料槽的喂入口开始，流经抛送叶轮、圆形外壳出口、出料直管和出料弯管。

首先使用三维建模软件Pro/E建立抛送叶轮的实体模型，然后将Pro/E所生成的叶轮三维实体模型导入到CFD的前处理软件GAMBIT中，并在GAMBIT中生成计算区域的实体模型，再对其进行网格划分。

考虑到计算区域的复杂性，将其分成了4个部分，分别是入口区、抛送叶轮区、圆形外壳区和出料管区（包括出料直管和出料弯管区域）。网格划分采用适应性较强的非结构化网格和混合网格。为了减少出料弯管下方出料口处的气流回流，增大了这个区域的计算体积。根据区域的大小及重要性采用大小不同的网格，整个区域共划分为481169个网格，如图4.1a所示。

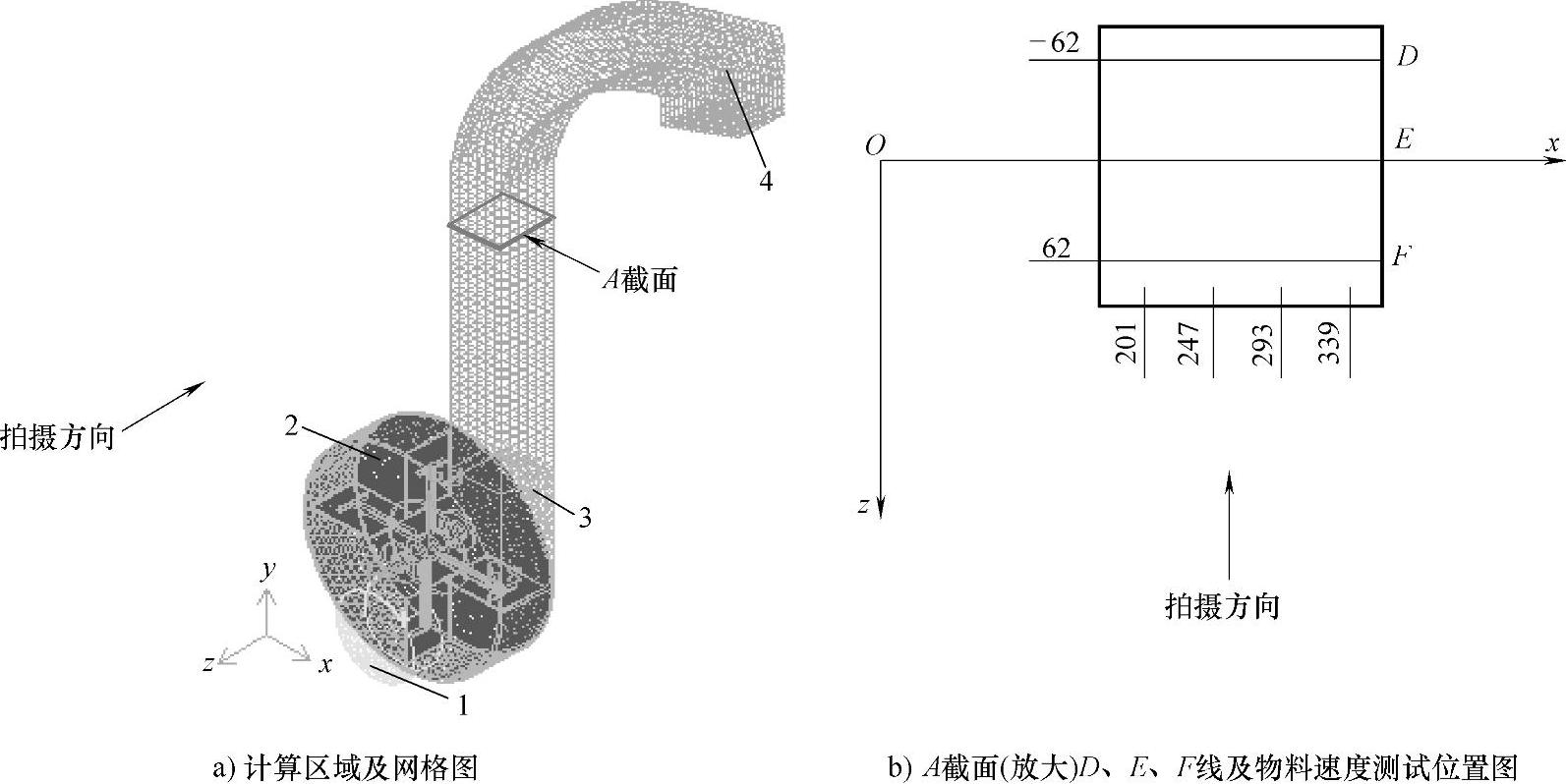
图4.1 叶片式抛送装置计算区域、网格以及物料速度测试位置图

4.边界条件和数值计算方法

计算时采用多重参考系（MRF）模型，抛送叶轮区域设在运动坐标系，转速为650r/min，其余区域设在固定坐标系处于静止状态。动、静两个区域的交界面处通过将速度转化成绝对速度的形式进行流场信息交换。计算区域的进口有3处，分别为进料口以及叶轮轴两侧轴承座旁的间隙面，均设为速度进口边界条件。其中进料口处气流和物料速度均为6.5m/s，物料的体积分数为0.2；叶轮轴两侧轴承座旁的两个间隙面处只有空气进入，空气流速度为1.5m/s，没有物料进入，所以设物料速度为0，物料的体积分数设为0。两个压力出口，均给定标准大气条件作为压力边界值，并假定进料口处物料体积分数均匀分布，等于物料输出体积分数。

采用有限体积法离散控制方程，对抛送装置内的三维定常流场进行分离式隐式求解。抛送装置大部分计算区域设在固定坐标系，所以计算时将单相流的标准k-ε模型扩展至多相流湍流模型。采用无滑移壁面边界条件，近壁区的流动模拟采用标准壁面函数，离散格式为二阶迎风格式，将单相流的压力速度耦合SIMPLEC算法扩展至气固两相流中。物料与气流之间的相对速度采用代数滑移（Manninen）公式；物料与气流之间的曳力函数采用Schiller-Naumann模型函数。