为了与高速摄像试验数据对比修正所建数学模型，首先利用MATLAB对物料沿出料直管及弯管运动的数学模型进行数值求解。求解之前，需将高阶微分方程简化为低阶微分方程，边界条件如图3.3所示。

1.高阶微分方程低阶化

（1）将式（3.5）、式（3.6）简化为低阶微分方程 将式（3.4）代入式（3.5），得

令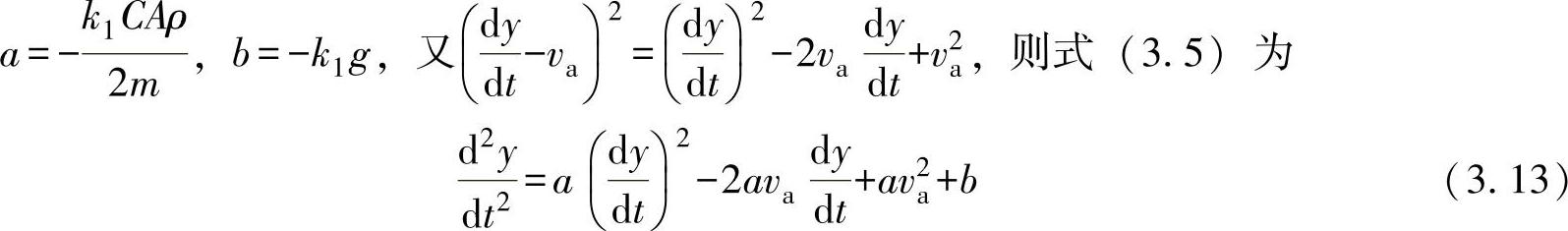

令c=-2av_a，d=av²_a+b，原方程为

边界条件为：t=0时，y=y₀₁，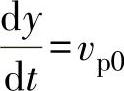

引入中间变量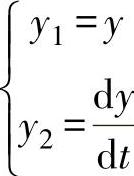，则原方程为

边界条件为y₁｜_t=0=y₀₁，y₂｜_t=0=v_p0。

式（3.6）的简化过程同上，只是系数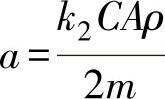，b=-k₂g，其他同上。

（2）将式（3.9）简化为低阶微分方程 引入中间变量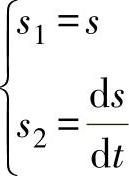，则原方程为

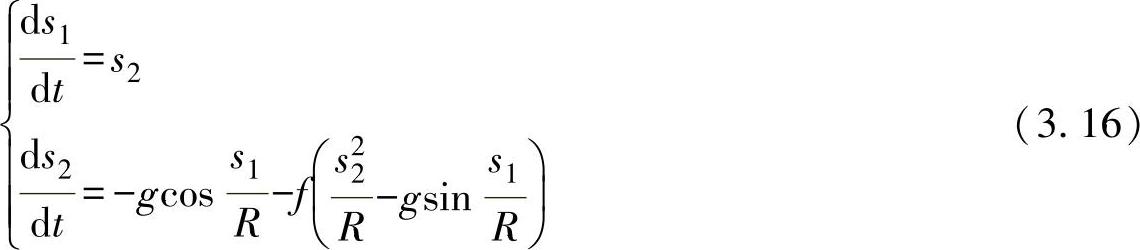
初始边界条件为s₁｜_t=0=Rα₀，s₂｜_t=0=v₀₂；终止边界条件为，。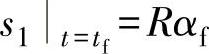

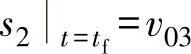（3）将式（3.10）简化为低阶微分方程

X方向：引入中间变量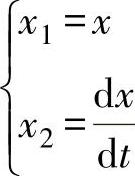，则原方程为

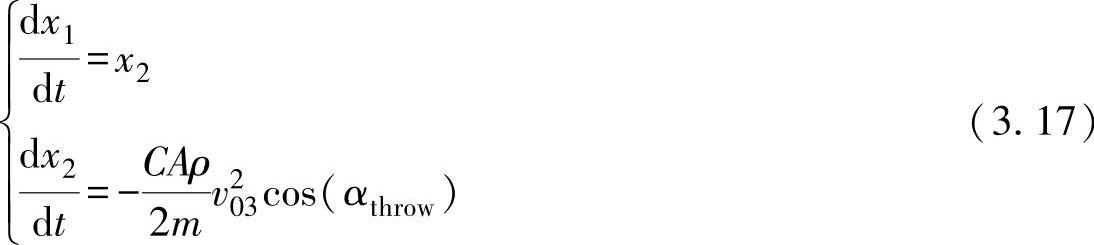
Y方向：引入中间变量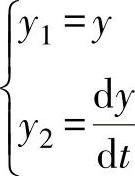，则原方程为

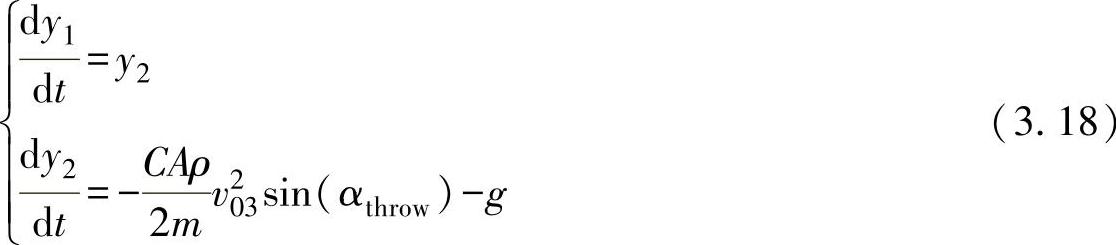
边界条件为

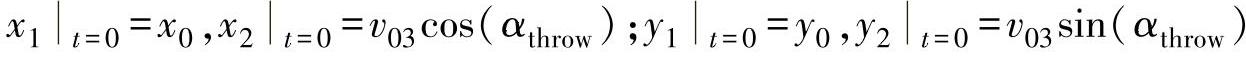
2.利用MATLAB进行数值求解

利用MATLAB进行数值求解时分五个阶段完成。

第一阶段为物料离开抛送叶片进入出料直管阶段，这阶段的初始条件为物料刚离开抛送叶片时的y坐标值、速度和出料直管处的平均气流速度，物料迎风面面积以及气流阻力系数等，利用MATLAB可求出出料直管各个位置物料的速度。

当物料速度小于气流速度时，就进入第二阶段，除系数a相差一个负号，阻力系数为k₂外，其他同第一阶段。

第三阶段为物料与外管壁碰撞阶段，要求输入碰撞前物料的初速度v₀₁以及摩擦因数f，出料弯管的几何形状及尺寸决定了碰撞角θ，利用MATLAB可求出碰撞后物料的速度v₀₂。

第四阶段为碰撞后物料沿外管壁弧线运动阶段，v₀₂为这一阶段的初速度，出料弯管的几何形状及尺寸确定了物料运动的初始及终止位置，利用MATLAB可计算出物料离开出料弯管的速度v₀₃。

第五阶段为物料离开喷嘴后的运动阶段，v₀₃为其初速度，输入物料的质量、气流参数后即可计算出物料的抛送距离。

下面以叶轮外径700mm、宽度160mm、转速650r/min、径向叶片、抛送青玉米秸秆切碎段，喂入量30kg/min为例进行分析，其他工况下抛送其他物料的计算及分析过程相同，故省略。将物料运动规律的高速摄像研究得到的物料离开叶片、流经出料直管的运动速度以及第2章获得的出料直管的平均气流速度作为边界条件。由于阻力系数k₁、k₂未知，分别将其通过给定变化范围，使用最小二乘回归分析法，以实测边界值与数值求解值的残差平方和最小为拟合条件，可得k₁=60.5，k₂=14.5，具体方法同3.3.1节物料沿叶片运动的ADAMS模型及修正中当量摩擦因数的计算方法相同。

利用MATLAB进行数值求解选取的坐标系如图3.3所示，求解程序略。

运行结果如图3.12～图3.14所示。图3.12所示为物料经过出料直管的位移及运动速度曲线，上方为v_p>v_a时的位移及运动速度曲线。由图3.12可以看出，当物料运动到y=-0.086m位置（图3.3中a—a截面下方，a—a截面坐标为y=-0.084m）时，物料速度已由28m/s下降到16.5m/s（即出料直管的平均气流速度），且由k₁=60.5可知，物料离开叶片后进入出料直管前，物料与圆形外壳及物料间由于碰撞及摩擦产生的阻力远远大于气流阻力和物料的重力，致使物料速度急剧下降；下方为v_p≤v_a时的位移及运动速度曲线，由图3.12可见，当物料运动到y=0.173m位置（图3.3中b—b位置）时，物料速度由16.5m/s下降到12.5m/s，且由k₂=14.5可知，物料在出料直管段由于碰撞及摩擦产生的阻力远远小于进入出料直管前，因此物料速度下降较缓慢。(www.daowen.com)

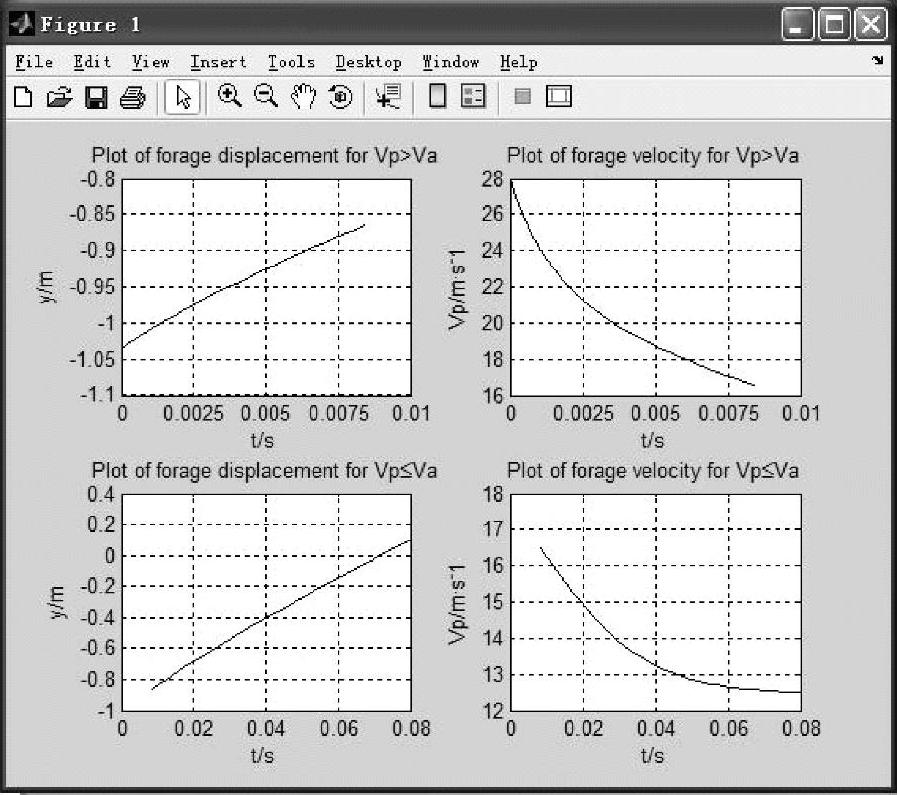
图3.12 物料经过出料直管的位移及速度曲线

图3.13所示为物料经过出料弯管的线速度曲线。由图3.13可见，物料与出料弯管碰撞后速度为7.14m/s，物料离开出料弯管时的速度为6.92m/s。

图3.14所示为物料离开出料弯管后的位移曲线。由图3.14可知，当y=-2.035m，即物料到达地面时，物料的抛送距离x=3.3m。数值计算结果与实测物料平均抛送距离3.496m基本一致。由此可见本章所建立的物料流经出料管的动力学模型以及MATLAB数值求解方法是正确可靠的。从而为出料直管及出料弯管几何参数的优化奠定了基础。

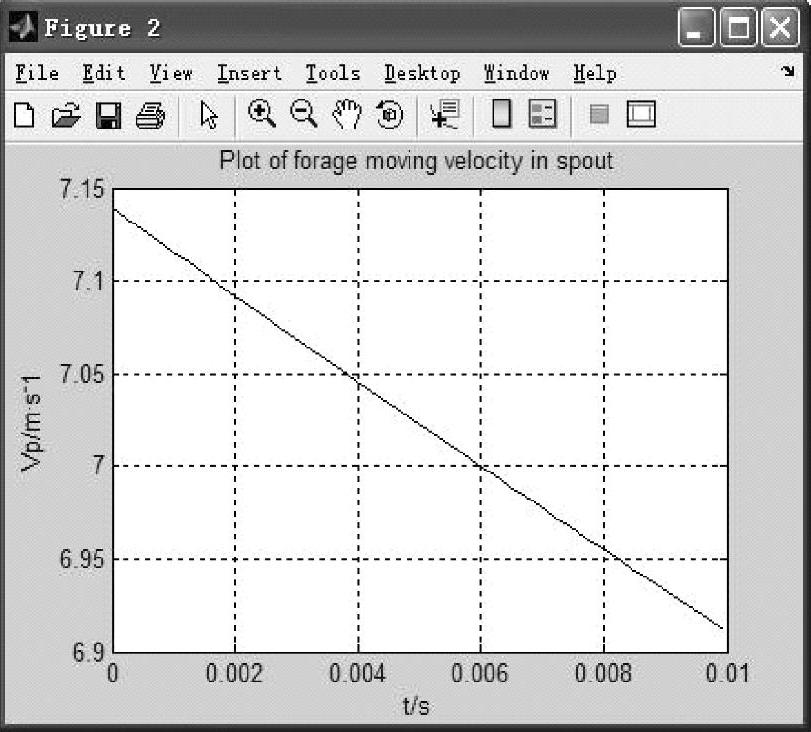
图3.13 物料经过出料弯管的线速度曲线

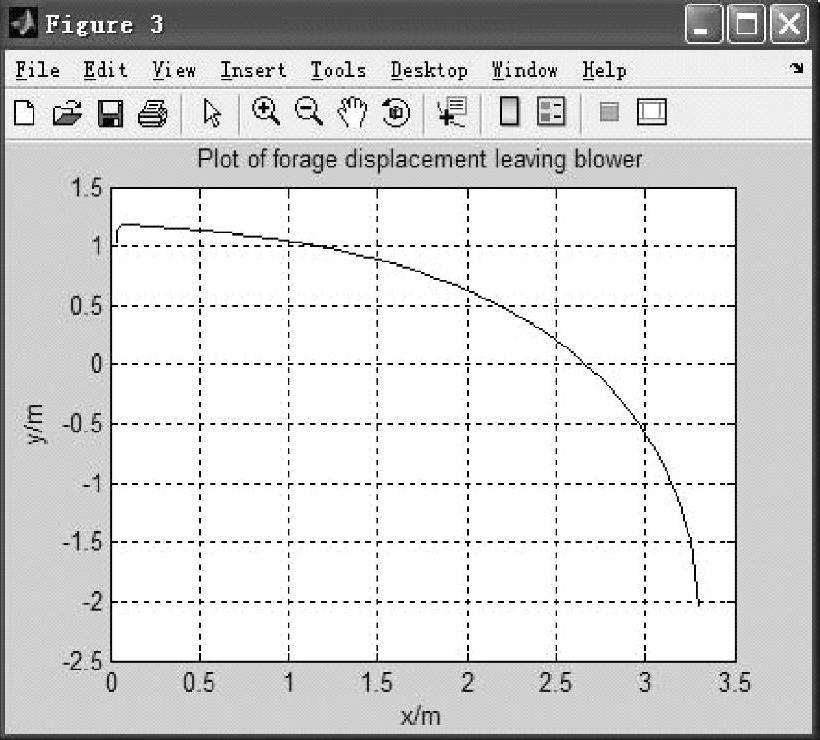
图3.14 物料离开出料弯管后的位移曲线

3.抛送距离试验

为了验证物料流经出料管动力学模型及MATLAB数值模拟结果，了解叶片式抛送装置抛送距离与结构及运动参数的关系，对各种设计参数下的抛送距离进行了试验研究。试验工况与2.6.2节的试验工况相同。

测试抛送距离时，在出料弯管的后面放置一块长11m，宽6m的防水布，在长度方向上每间隔1m划一条线，将防水布分成11个部分。每次试验后，将抛在防水布每部分上的物料称重、记录后按下式计算其平均抛送距离和标准偏差。

式中 x_m——平均抛送距离（m）；

s_m——标准偏差（m）；

M_i——每部分（每米）范围内的物料质量（kg）；

x_i——每部分中点的抛送距离（m）。

重复试验3次，取其平均值。抛送试验的结果见表3.2～表3.5。

表3.2 叶轮外径ϕ700mm，叶片宽160mm，各叶片倾角的平均抛送距离和标准偏差

表3.3 叶轮外径ϕ700mm，叶片宽度160mm，径向叶片时各转速的平均抛送距离和标准偏差

表3.4 叶轮外径ϕ600mm，叶片宽度150mm，径向叶片时各转速的平均抛送距离和标准偏差

表3.5 叶轮外径ϕ500mm，叶片宽度140mm，径向叶片时各转速的平均抛送距离和标准偏差

当叶轮外径为700mm、宽度为160mm、转速为650r/min、喂入量为30kg/min时平均抛送距离与叶片倾角的关系如图3.15所示。图3.16所示为径向叶片时不同叶轮外径、宽度及喂入量下平均抛送距离与叶轮转速的关系曲线。由图3.15可知当叶轮外径为700mm、宽度为160mm、转速为650r/min、喂入量为30kg/min时，后倾角为10°的叶片平均抛送距离最远；由图3.16可见，在相同叶轮外径、宽度及喂入量下，转速越高，平均抛送距离越远。

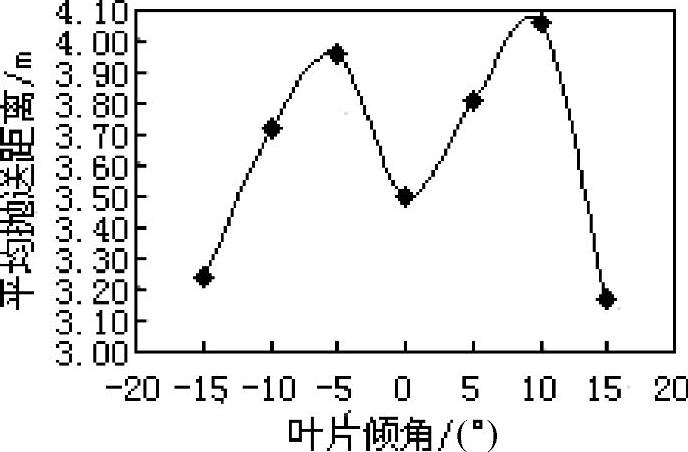
图3.15 平均抛送距离与叶片倾角的关系

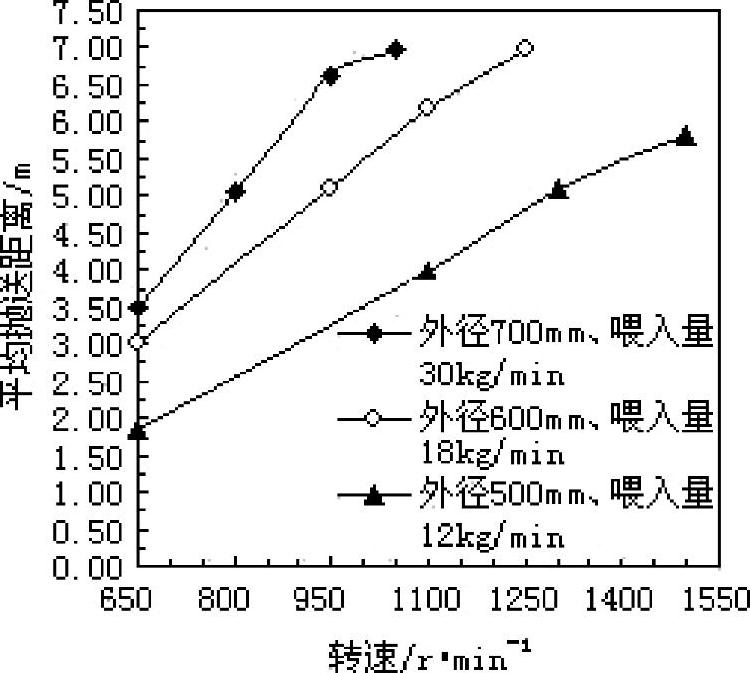
图3.16 平均抛送距离与转速的关系

结合第2章2.6.4节的试验结果（图2.9～图2.10）可知，物料的抛送距离与出料直管A截面的气流速度密切相关，气流速度越大，物料的平均抛送距离越远。