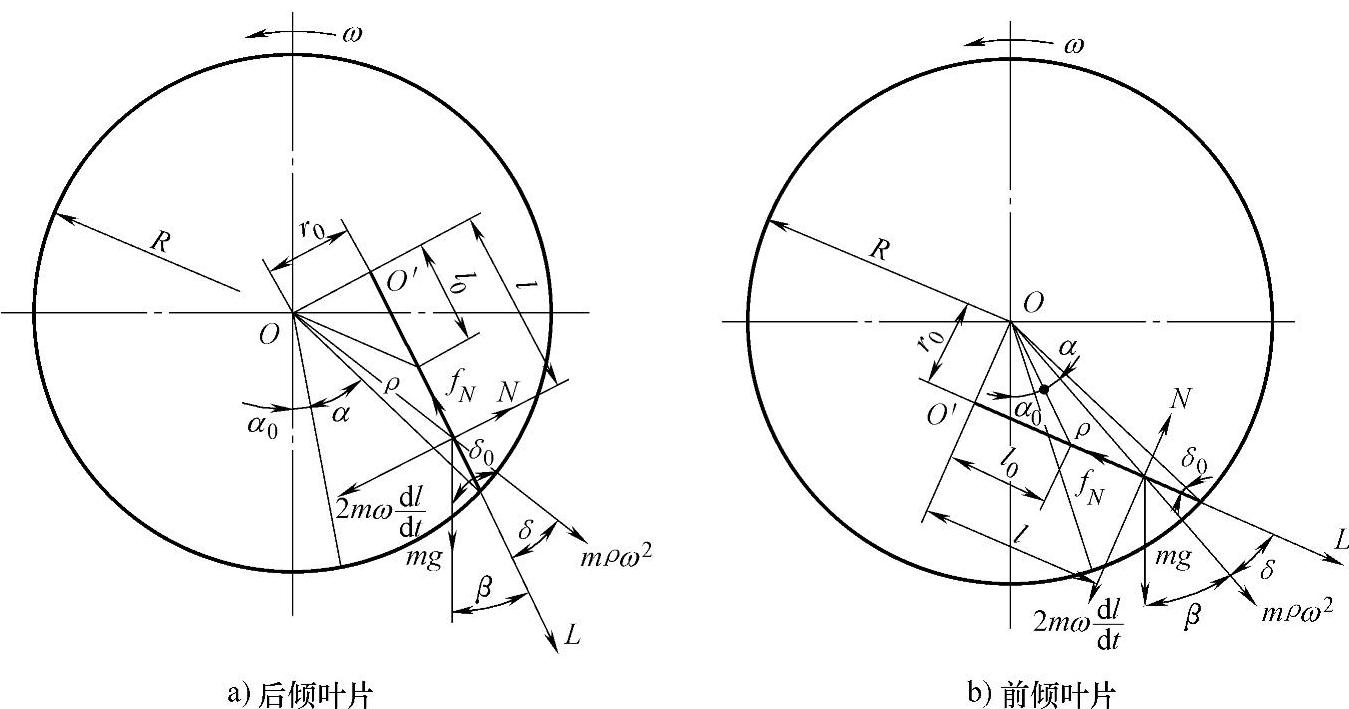
图3.1 物料质点沿叶片滑移过程中的受力状况

物料质点沿叶片滑移过程中的受力状况如图3.1所示，作用于物料质点的力有重力mg、离心力mρω²、哥氏力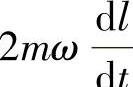、叶片法向反力N以及摩擦力f_N。转轴O水平配置，动坐标轴O′L沿叶片方向向外为正并与叶片一起旋转，由O向O′L作垂线，交点O′为动坐标原点。

为了建立物料质点沿叶片运动的动力学方程，做以下几点假设：

1）物料与叶片之间的碰撞为非弹性碰撞。

2）物料与叶片碰撞后沿叶片滑移的初速度为零。

3）抛送叶片处气流对物料的作用忽略不计。

4）抛送叶轮以等角速度ω旋转。

当抛送装置正常工作时，物料质点沿叶片运动的动力学方程为[33]：

由此可得物料质点沿叶片运动的微分方程[16，33]：

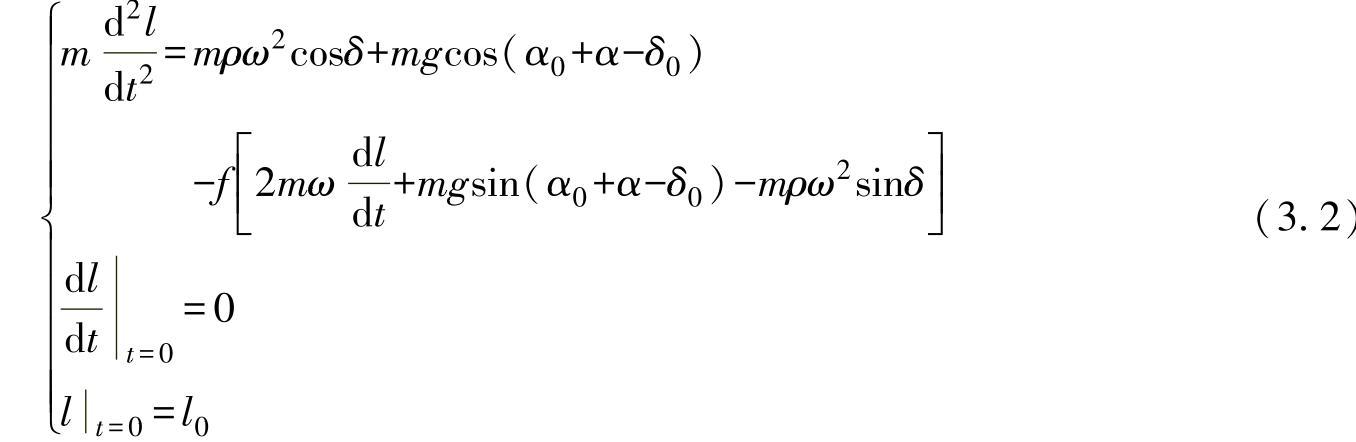
解上述方程，得

l=C₁e^λ1t+C₂e^λ2t+Dcos（ωt+α₀）+Msin（ωt+α₀）-fr₀ （3.3）

其中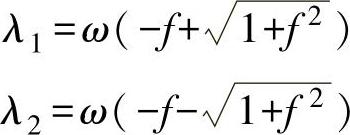

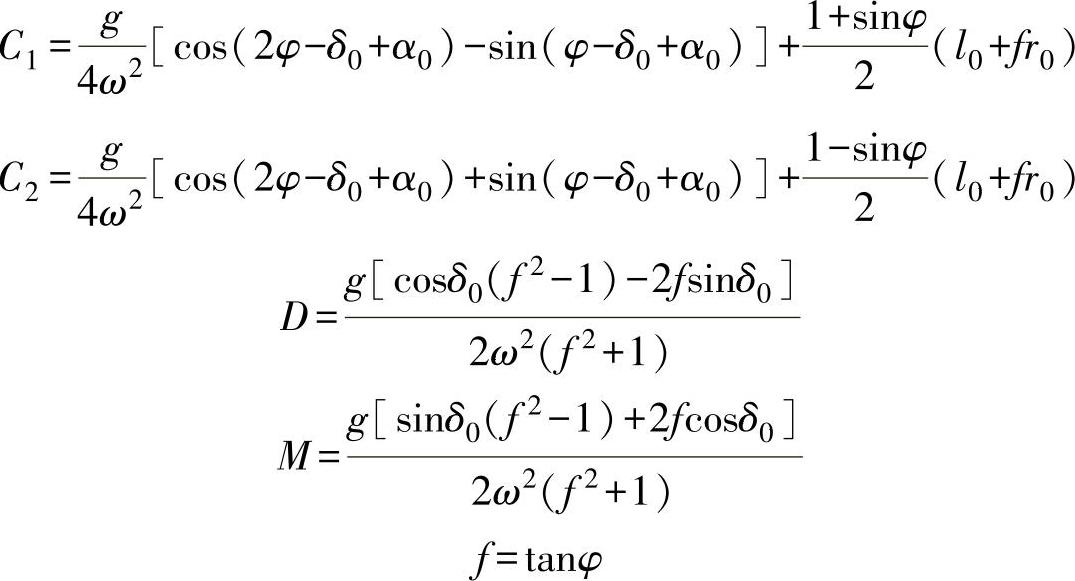
式中 t——时间（s）；(www.daowen.com)

m——物料质量（kg）；

g——重力加速度（mm·s^-2）；

ω——叶轮角速度（rad·s^-1）；

r₀——两坐标原点OO′之间的位移（mm）；

ρ——物料质心所在位置与叶轮轴心O的距离（mm），r₀=ρsinδ；

l——物料质点动坐标（mm）；

l₀——物料质点初始位置的坐标（mm）；

R——叶轮外半径（mm）；

δ——叶片与径向夹角（°）；

δ₀——叶片安装角（°），规定径向叶片倾角为零，后倾叶片倾角为正，前倾为负；

α——叶片转角（°），α=ωt；

α₀——初相位（°），即叶片初始位置与纵轴夹角；

β——叶片与重力方向的夹角（°），β=α₀+α-δ₀；

f——物料与叶片的摩擦因数；

φ——摩擦角（°），φ=arctanf。