一、点的投影

点是组成立体最基本的几何元素，为了准确地表达物体的结构形状，应首先掌握点的投影规律及作图方法。

1.点的三面投影标记

点的投影永远是点。

过空间点A分别向三个投影面V、H、W作垂线，垂足即点A在三个投影面上的投影，分别用标记a′、a、a″表示，如图3-18a所示。

规定空间点及其投影的标记：空间点用大写字母A、B、C、…表示，H面投影用相应的小写字母a、b、c、…表示，V面投影用相应的小写字母加一撇a′、b′、c′、…表示，W面投

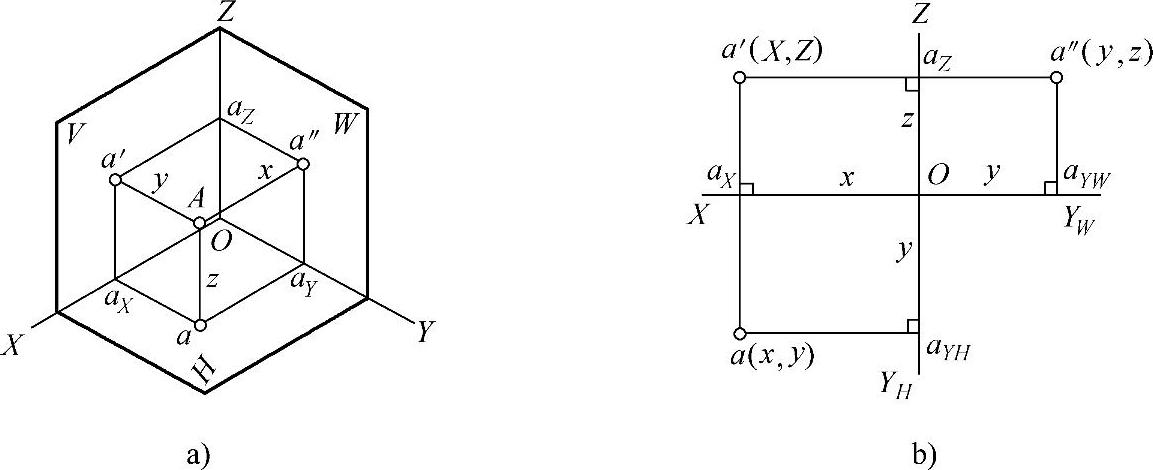
图3-18 点的投影

a）点的空间位置 b）点的三面投影

影用相应的小写字母加两撇a″、b″、c″、…表示。

2.点的投影规律

将三投影面体系按三视图同样的方式展开，得到点A的三面投影如图3-18b所示。由点的投影的形成和展开过程得出点的投影规律如下：

1）点A的正面投影和水平投影的连线垂直于OX轴，即a′a⊥OX。

2）点A的正面投影和侧面投影的连线垂直于OZ轴，即a′a″⊥OZ。

3）点A的水平投影a到OX轴的距离等于点A的侧面投影a″到OZ轴的距离，即aa_x=a″a_Z；作图时可以用圆弧或45°斜线反映它们之间的投影关系。

【小提示：】

对照三视图的投影规律可以看出，点的投影规律与三视图的投影规律是一致的。

由点的投影规律可知，已知点的两面投影，可以求出第三面投影。

【例3-1】 已知点B的正面投影b′和水平投影b，求其侧面投影b″。

作图步骤如图3-19a所示。

【例3-2】 已知点C的正面投影c′和侧面投影c″，求其水平投影c。

作图步骤如图3-19b所示。

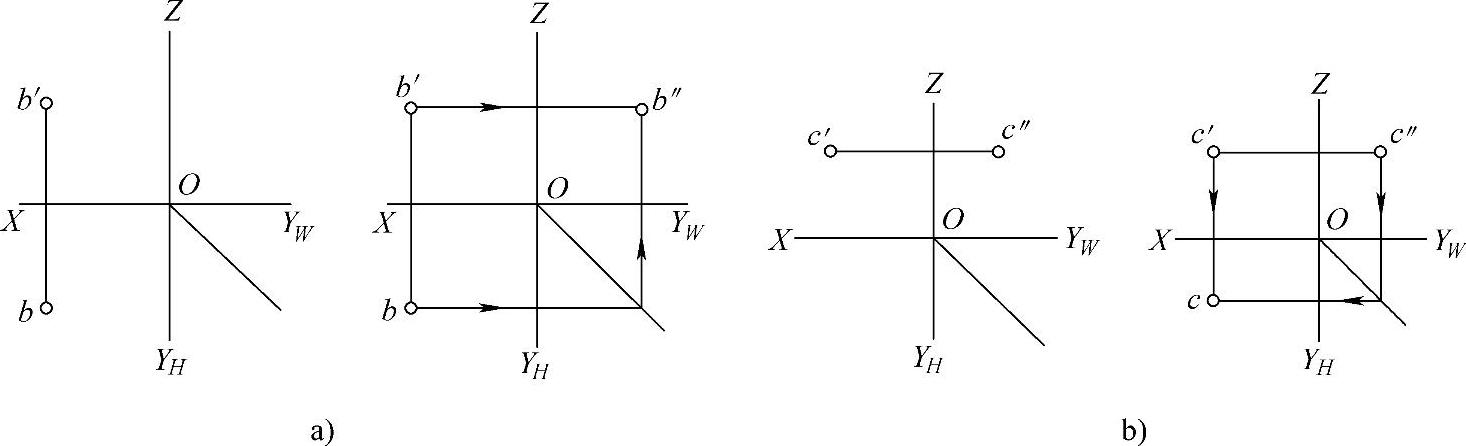
图3-19 点的二求三作图

3.点的投影与坐标的关系

任何一个点A在空间的位置都是由点的x、y、z三个坐标决定的，即点A（x，y，z）。由图3-18a可知，空间点A（x，y，z）的坐标决定了点A到投影面的距离。

1）点的x坐标等于点A到W面的距离。

2）点的y坐标等于点A到V面的距离。

3）点的z坐标等于点A到H面的距离。

由图3-18b可知，空间点在某一投影面上的投影是由点的两个坐标决定的。因此，已知点的坐标，同样可以求出点的三面投影。

【例3-3】 已知点A（15，12，20），求点的三面投影。

作图步骤如图3-20所示。

4.两点的相对位置

空间两点的相对位置有两种判断方法：一是根据两点的同面投影来判断，其上、下、前、后、左、右位置与三视图的方位关系。二是根据两点的坐标来判断：x坐标决定点的左右位置，x坐标大的点在左；y坐标决定点的前后位置，y坐标大的点在前；z坐标决定点的上下位置，z坐标大的点在上。

如图3-21所示的空间点A、B，由正面投影可判断出A在B的上、左方；由水平投影可判断出A在B的左、前方，由侧面投影可判断出A在B的前、上方，因此，由三面投影或两投影就可以判断点A在点B的左、前、上方。

图3-20 根据点的坐标求点的三面投影

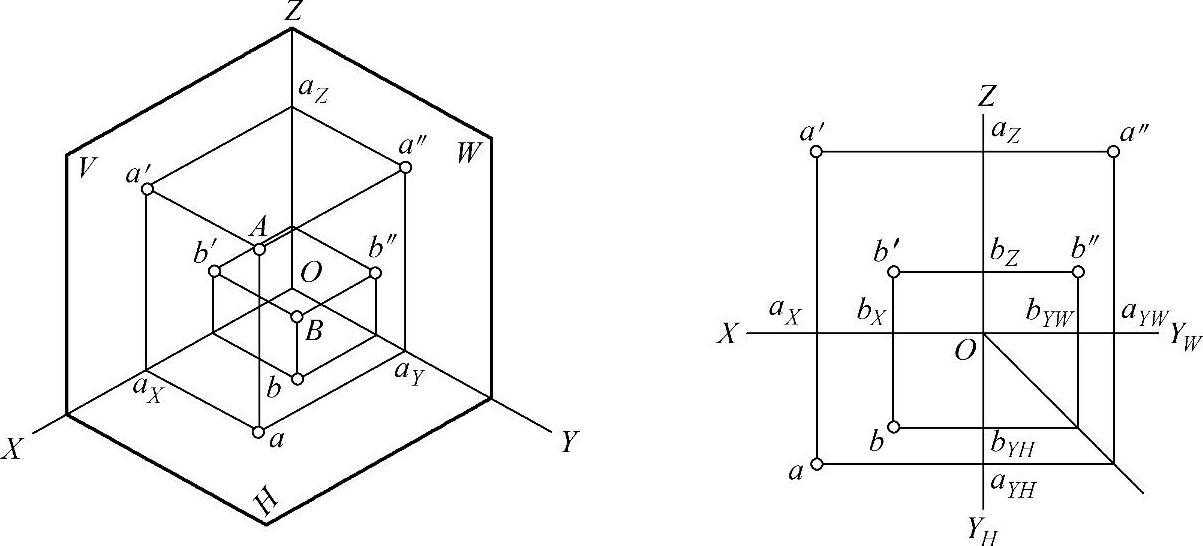
图3-21 两点的相对位置

5.重影点

如果空间两点有两个坐标相等，一个坐标不相等，则两点在一个投影面上的投影就重合为一点，这两点称为该投影面的重影点。如图3-22所示，点B在点A的正下方，则两点A、B是水平面的重影点。

重影点要判别投影的可见性，方法是：比较两点不相同的那个坐标，其中坐标大的可见。例如，A、B两点的x和y坐标相同，z坐标不等，因a_z＞b_z，因此，a可见，b不可见，不可见点的投影应加括号，如图3-22所示。

二、直线的投影

直线也是构成物体的基本几何元素。如图3-23所示的棱锥就是由不同位置的八条棱线构成的。

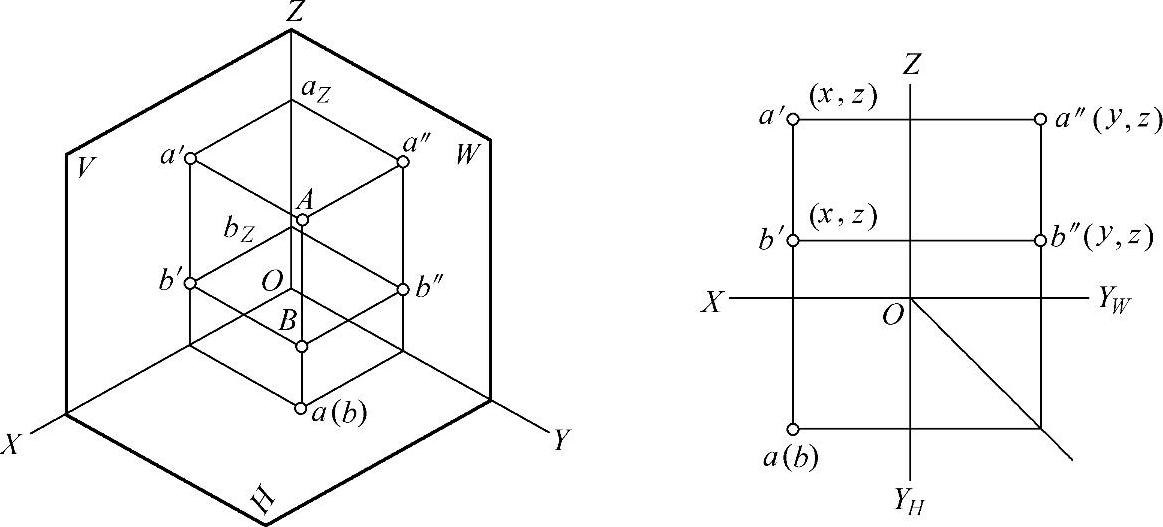
图3-22 重影点

两点确定一条直线，因此，直线的投影就是直线上两点同面投影的连线。如图3-23所示，直线MN的投影就是直线上两端点M、N的同面投影m′、n′，m、n，m″、n″的连线。直线的投影一般仍是直线。

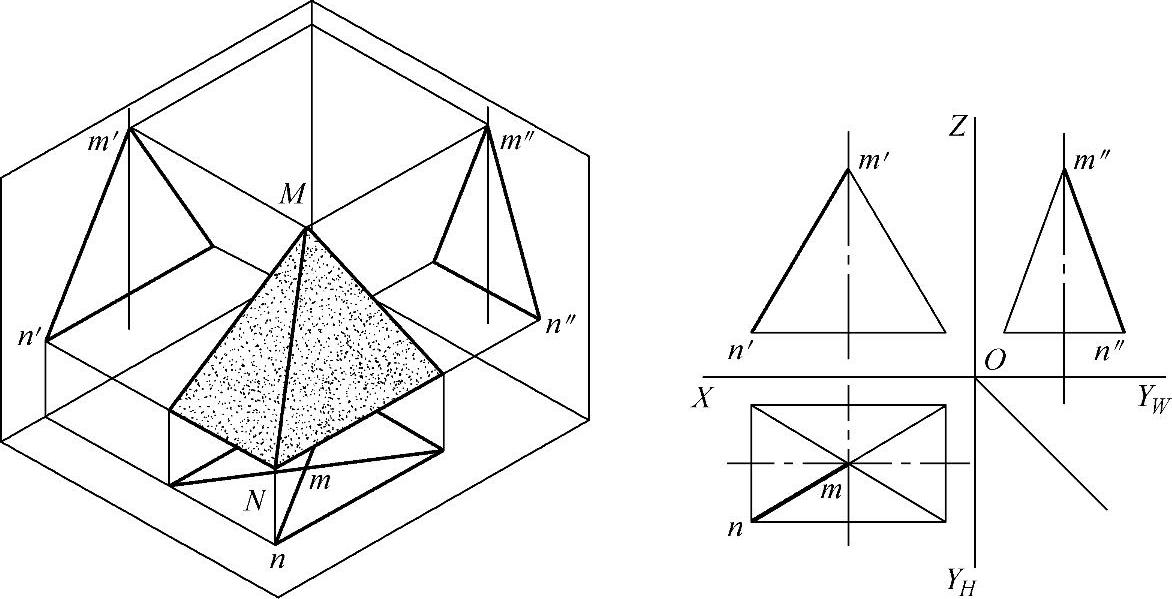
图3-23 直线的投影

按照直线相对于三个投影面的位置不同，可以把直线分为三种：一般位置直线、投影面平行线、投影面垂直线。后两种直线又称为特殊位置直线。

1.一般位置直线

与三个投影面都倾斜的直线称为一般位置直线。如图3-23所示，直线MN就是一般位置直线。

由图3-23可知，一般位置直线的投影特性如下：

1）三面投影都倾斜于投影轴。

2）三面投影均小于实长。

即一般位置直线的三面投影都是小于实长的斜线，简称“三斜”。

2.投影面平行线(www.daowen.com)

平行于一个投影面，与另两个投影面倾斜的直线称为投影面平行线。

投影面平行线有三种：

1）正平线——平行于V面，如图3-24中的直线AB。

2）水平线——平行于H面，如图3-24中的直线CD。

3）侧平线——平行于W面，如图3-24中的直线EF。

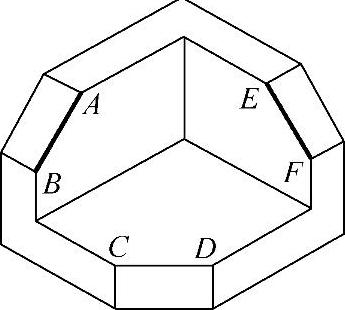
图3-24 投影面平行线

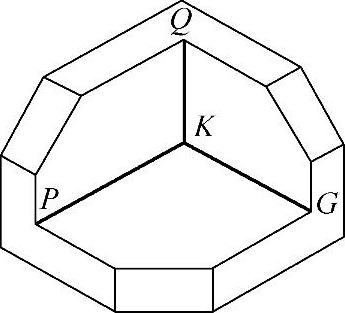
图3-25 投影面垂直线

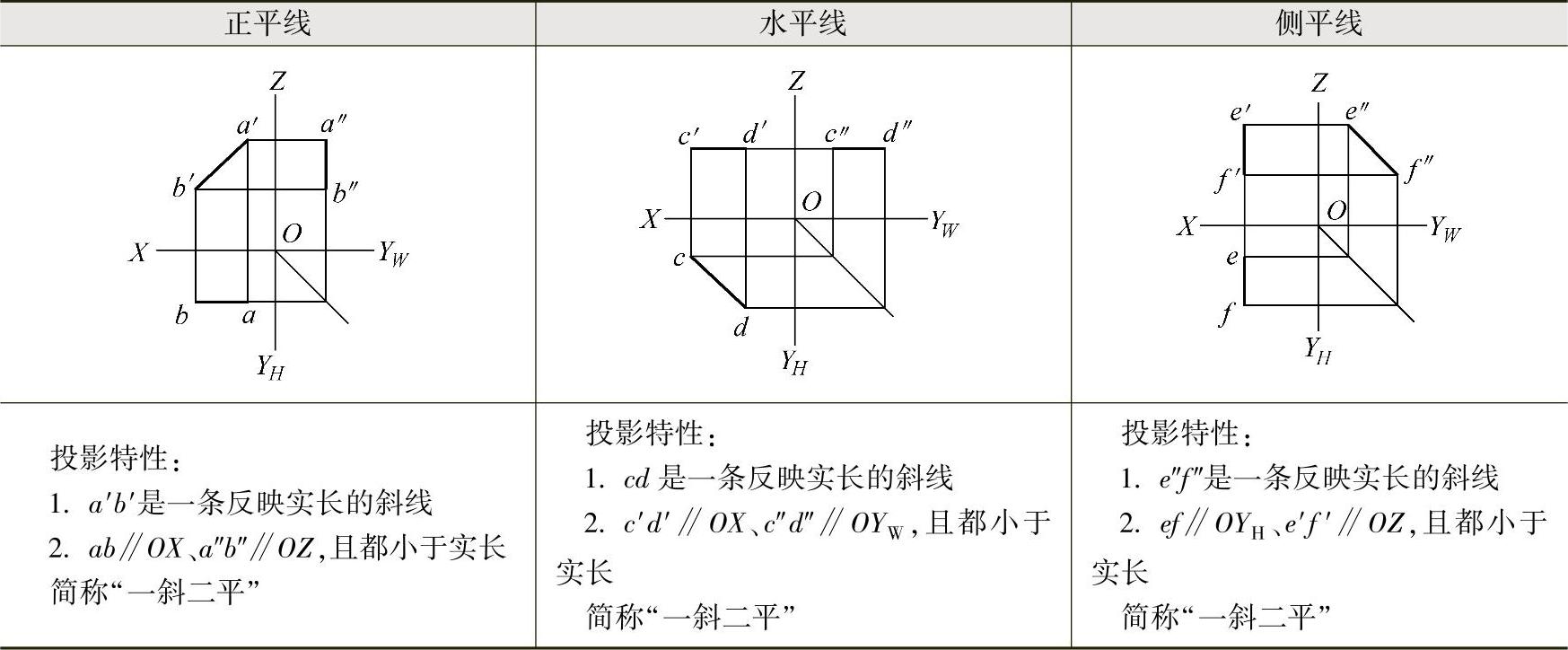
投影面平行线的投影特性见表3-1。

表3-1 投影面平行线的投影特性

3.投影面垂直线

垂直于一个投影面，平行于另外两个投影面的直线称为投影面垂直线。

投影面垂直线有三种：

（1）正垂线——垂直于V面，如图3-25中的直线GK。

（2）铅垂线——垂直于H面，如图3-25中的直线QK。

（3）侧垂线——垂直于W面，如图3-25中的直线PK。

投影面垂直线的投影特性见表3-2。

表3-2 投影面垂直线的投影特性

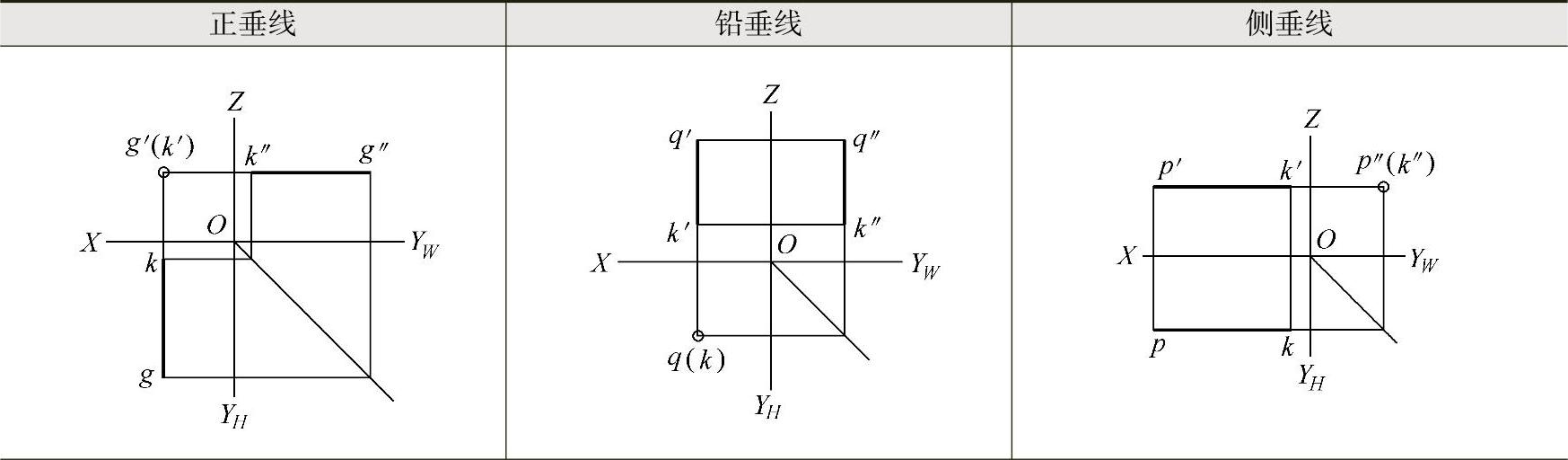
（续）

三、平面的投影

平面可以看做由若干个点组成，或由几条直线构成，因此，平面的投影同样可以由点的同面投影的连线求出，如图3-26所示。

按照平面相对于三个投影面的位置不同，可以把平面分为三种：一般位置平面、投影面垂直面和投影面平行面。后两类平面又称为特殊位置平面。

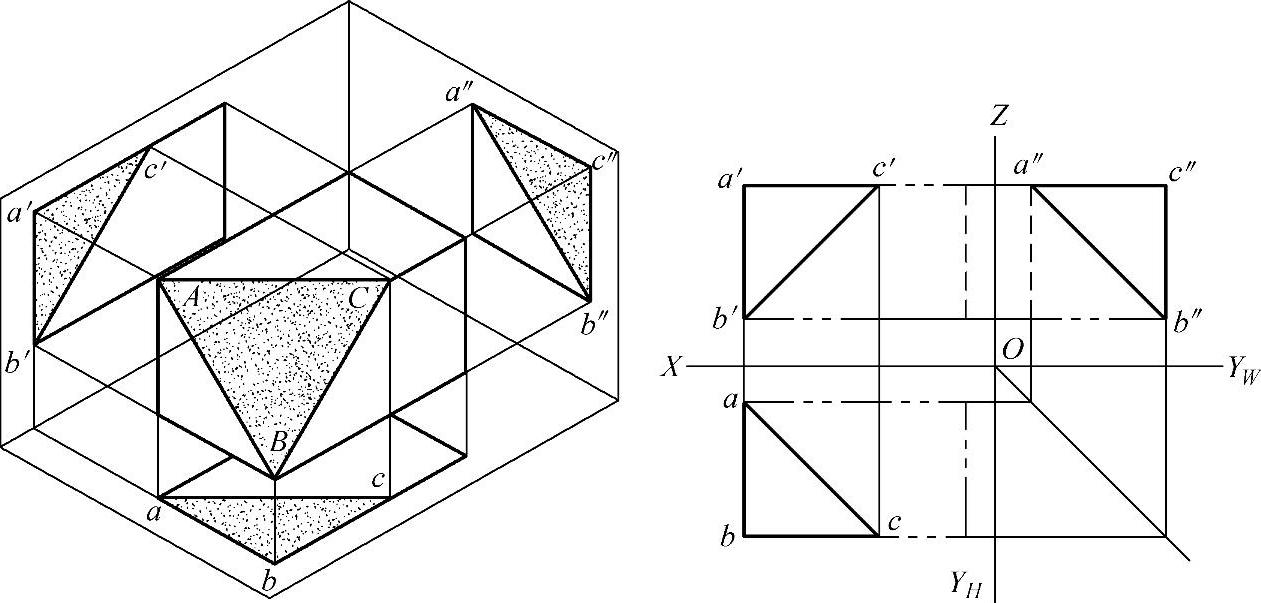
图3-26 平面的投影

1.一般位置平面

与三个投影面都倾斜的平面称为一般位置平面。图3-26的△ABC的平面就是一般位置平面。

由图3-26可知，由于△ABC对H、V、W面都倾斜，因此它的三个投影都是小于实形的类似形。

2.投影面垂直面

垂直于一个投影面，与另两个投影面倾斜的平面称为投影面垂直面。

投影面垂直面分为三种：

1）正垂面——垂直于V面，如图3-27中的A面。

2）铅垂面——垂直于H面，如图3-27中的B面。

3）侧垂面——垂直于W面，如图3-27中的C面。

投影面垂直面的投影特性见表3-3。

表3-3 投影面垂直面的投影特性

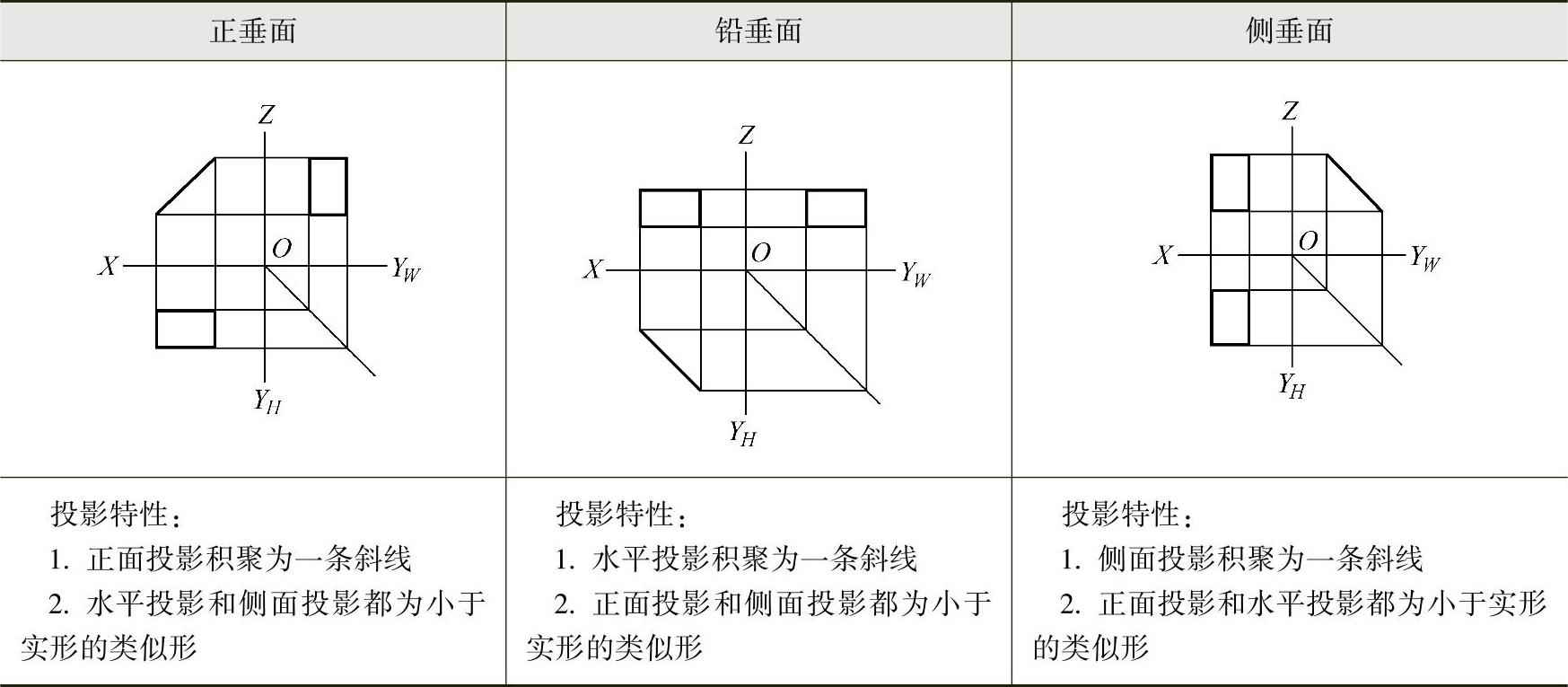
3.投影面平行面

平行于一个投影面，与另两个投影面垂直的平面称为投影面平行面。

投影面平行面分为三种：

1）正平面——平行于V面，如图3-28中的A面。

2）水平面——平行于H面，如图3-28中的B面。

3）侧平面——平行于W面，如图3-28中的C面。

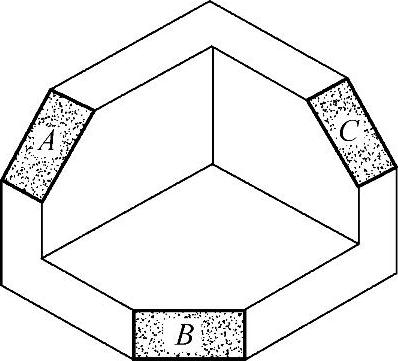
图3-27 投影面垂直面

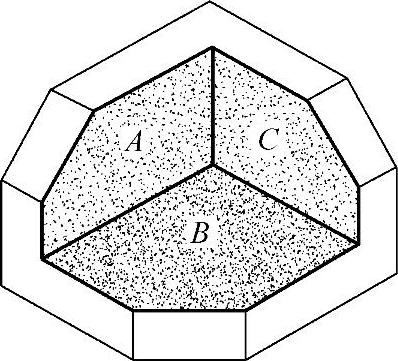
图3-28 投影面平行面

投影面平行面的投影特性见表3-4。

表3-4 投影面平行面的投影特性

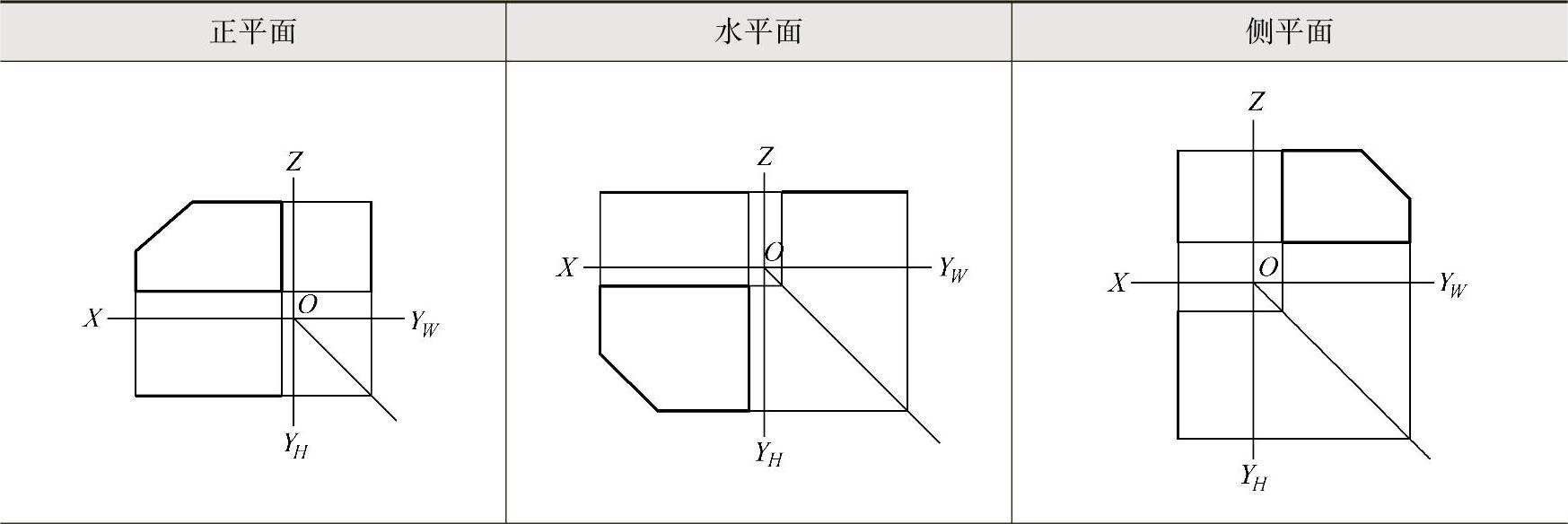
（续）