线性预测分析的基本原理是将被分析的信号用一个模型来表示，即将信号看作某一个模型的输出。这样，就可以用模型参数来描述信号。图9-2 是信号s（n）的模型化框图。图中u（n）表示模型的输入，s（n）表示模型的输出。对于确定性信号，输入采用单位冲激序列；对于随机信号，输入采用白噪声序列。

图9-2　信号模型

模型的系统函数H（z）可以写成有理分式的形式，即

其中，系数ai、bl 增益因子G 就是模型的参数；而p 和q 是模型的阶数。因而，信号可用有限数目的参数构成的模型来表示。可得模型输入与输出之间的时域关系为

其中，b0=1。这是一个线性常系数差分方程。模型的输出是模型过去的输入、当前的输入及过去输出的线性组合。这表明，当模型参数设计好后，就可以用模型的输入及过去的信号值来估计当前的信号值。

根据H（z）的不同形式，有如下3 种不同的信号模型。

1.所示的H（z）同时含有极点和零点，称为自回归-滑动平均模型，简称为ARMA（Auto Reressive Moving Average）模型，这是一种一般模型。

2.当分子多项式为常数，即bl=0。时，H（z）为全极点模型。这时，模型的输出只取决于过去的信号值，这种模型称为自回归模型，简称为AR（Auto Regressive）模型。

3.如果H（z）的分母多项式为1，H（z）为全零点模型，称为滑动平均模型，简称为MA（Moving Average）模型。此时，模型的输出只取决于模型的输入。

实际上，最常用的模型是全极点模型，原因如下。

1.全极点模型最容易计算，对全极点模型做参数估计就是求解线性方程组，相对来说比较容易。而若模型中含有有限个零点，则是解非线性方程组，实现起来非常困难。

2.有时无法知道输入序列，如对于一些地震应用、脑电图及解卷积等问题。

3.如果不考虑鼻音和摩擦音，那么语音的声道传递函数就是一个全极点模型。

而对于鼻音和摩擦音，声学理论表明，其声道传输函数既有极点又有零点。这时，如果模型的阶数p 足够高，可以用全极点模型来近似表示零极点模型。因为一个零点可以用许多个极点来近似，即

如果分母多项式收敛得足够快，只取其少数几项就够了。所以，用全极点模型为实际应用提供了合理的近似。在语音线性预测方面的文献和资料中，绝大多数情况就是采用这种全极点模型，故以后主要讨论全极点模型。

（一）建立线性预测方程

模型的建立，实际上是由信号估计模型参数的过程，由于信号是客观存在的，用模型表示它不可能完全精确，总存在误差。极点阶数p 和零点阶数q 无法事先确定，可能选得过大或过小，况且信号是时变的。因此，求解模型参数实际上是一个逼近过程。

对于全极点模型，有

s（n）和u（n）之间的关系可用差分方程表示为

其中

称为线性预测器。式中，ai 称为线性预测系数。因为它是由s（n）邻近的过去p 个值线性组合得到的，即由s（n）过去的值来预测或估计当前值s（n）。

p 阶线性预测器的系统函数可表示为

信号值s（n）与线性预测值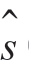（n）之差称为线性预测误差，用e（n）表示，即(www.daowen.com)

可知，预测误差序列是输入为s（n）且具有如下系统函数的系统输出，即

因而，可以定义预测误差滤器A（z），它就是模型H（z）的逆滤波器，因此，H（z）可表示为

其中，A（z）称为逆滤波器，其物理意义就是进行反向线性预测。

线性预测的基本问题是由语音信号直接确定一组预测器系数{ai}，使预测误差在某个准则下最小，这个准则通常采用最小均方误差准则，这一过程称为线性预测分析。

下面推导线性预测方程。预测平方误差为

由于语音信号的时变特性，预测器系数的估计必须在一段语音信号中进行，因而取和的间隔是有限的。另外，为了取平均，求和式应该除以语音段的长度。然而，这个常数和将要得到的线性方程组无关，因而将其忽略。

为使E 最小，各系数ai 应满足E 对ai 的偏微分为0，即

有

即得到线性预测的标准方程组，线性方程组为

如果定义

则本式可以简写成

本式是由p 个方程组成的含有p 个未知数的方程组，求解方程组可得各个预测器系数a1，a2，…，ap。可得最小均方误差，即

或可表示为

因此，最小误差由一个固定分量和一个依赖预测器系数的分量组成。

为求解最佳预测器系数，必须首先计算Φ（i，j）（1 ≤ i≤ p，1 ≤ j ≤ p）。一旦求出这些数值，即可求出ai。因此，从原理上看，线性预测分析是非常直截了当的。然而，Φ（i，j）的计算及方程组的求解十分复杂。

（二）语音信号的线性预测分析

根据前面介绍的模型化思想，可以对语音信号建立模型，如图9-3 所示。

从图9-3 可知，该模型是语音产生模型的一种特殊形式，它将其中的辐射、声道以及声门激励的全部谱效应简化为一个时变的数字滤波器来等效，其系统函数为

图9-3　语音信号模型

这样将s（n）模型转化为一个p 阶AR 模型。图9-3 所示的模型常用来产生合成语音，故滤波器H（z）也称作合成滤波器。该模型参数包括浊音/清音判决、浊音语音的基音周期、增益常数G 及数字滤波参数ai。当然，这些参数都是随时间缓慢变化的。采用这样一种简化模型，其主要优点在于能够用线性预测分析方法对滤波器系数ai 和增益常数G 进行非常直接和高效的计算。

在图9-3 所示的模型中，数字滤波器H（z）的参数ai 就是前面定义的线性预测系数。因此，求解滤波器参数和G 的过程称为语音信号的线性预测分析。其基本问题就是从语音信号序列中直接确定一组线性预测系数{ai}。鉴于语音信号的时变特性，预测系数的估计值必须在一段语音信号中进行，即按帧进行。

这种简化的全极点模型对于非鼻音浊音语音是一种合乎自然的描述，而对于鼻音和摩擦音，理论上应该采用零极点模型，而不是简单的全极点模型。