【摘要】:现在把前面介绍的算法推广到辨识ARMA 过程的参数上,ARMA 过程或用Z差分方程描述,或用变换来描述,即可将式中右边的传递函数用全极点传递函数来近似,其方法是用足够多的极点数来代替每个零点。为了确定近似的AR 模型参数{ri}与对应的ARMA 模型参数{αi}和{βi}之间的关系,得交叉相乘,得使z 的同幂项的系数相等,得出以下方程组当j=M+1,M+1,…另一方面,利用卡尔曼型算法求参数{ri}时,N′阶模型必须是事先确定的。令和表示假设的N 和M 值。
现在把前面介绍的算法推广到辨识ARMA 过程的参数上,ARMA 过程或用Z差分方程描述,或用变换来描述,即
可将式中右边的传递函数用全极点传递函数来近似,其方法是用足够多的极点数来代替每个零点。把一个零点写成
就可看清这一点。在多数应用中,只要用级数的前面几项就足够了。因此,我们能够用纯AR 过程对ARMA 过程x(k)进行近似。方法是将式的右边写成
当N′=∞时,得到严格的等效,对有限的N 近似也是很好的。一般地,N′ ≥N+M。
为了确定近似的AR 模型参数{ri}与对应的ARMA 模型参数{αi}和{βi}之间的关系,得
交叉相乘,得
使z 的同幂项的系数相等,得出以下方程组
当j=M+1,M+1,…,N 时,βi=0。这些方程可写成矩阵形式,即(www.daowen.com)
和
上式代表一组M 个未知数的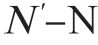 个方程组。为了求解,必须选N′=N+M。于是,一旦辨识出参数r1,…,rN',就能去求参数集合{αi}和{βi}。参数ri 用前面介绍的无论哪种方法都可辨识出来。辨识与{ri}有关的偏相关系数的好处是:N′阶模型不需要事先固定,可由计算方案求出。另一方面,利用卡尔曼型算法求参数{ri}时,N′阶模型必须是事先确定的。
个方程组。为了求解,必须选N′=N+M。于是,一旦辨识出参数r1,…,rN',就能去求参数集合{αi}和{βi}。参数ri 用前面介绍的无论哪种方法都可辨识出来。辨识与{ri}有关的偏相关系数的好处是:N′阶模型不需要事先固定,可由计算方案求出。另一方面,利用卡尔曼型算法求参数{ri}时,N′阶模型必须是事先确定的。
无论用哪种方案,仍然会留下确定相对阶数N 和M 的问题。令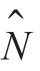 和
和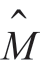 表示假设的N 和M 值。用
表示假设的N 和M 值。用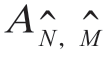 表示方阵,
表示方阵,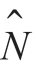 和
和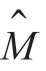 的值检验
的值检验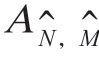 的秩,使
的秩,使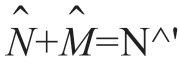 ,直到某个
,直到某个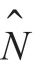 和
和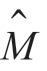 满足
满足
或变化为
如果N 和M 的估计偏低,就有可能(实质上在信号描述中)略去一些变化。另一方面,如果对N 和M 估计过大,在模型中会引入可以忽略不计的系数,这相当于加上了小幅度的高频项,在大多数应用时并不会产生计算问题。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关现代信号检测技术与评估理论的应用与研究的文章







