设模型阶数为n，相应的估计用 表示，即

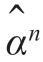而估计 满足

将方程的次序倒一下还可写成

现在令模型阶数加1，并令相应的估计为

于是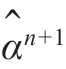， 满足

写为如下分块矩阵形式

和

以相关矩阵ΦN 的逆前乘式，可写出

的递推形式。当给定n 阶模型的估计时就能递推算出任何n+1 阶模型的估计。把这些方程重新按以下形式写出，就可明显看出这一点。令pn+1 代表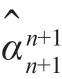，就能写出

其中

参数p 叫作偏相关系数。可清楚地看出，如果知道p1，…，pn，就能算出任何n 时的估计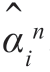。现在，来考虑求这些系数。令 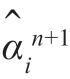乘以z-i，对i 求和，得

定义多项式

和

利用这些多项式，写为

现在用Fn（z-1）和Gn（z-1），求Gn+1（z-1）的关系。为此，用n+1-i 代替i，写为

得

进而就能得到如图9-1 所示的网格结构。

图9-1　用Levinson 算法进行辨识

由图9-1 可知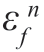，（k）为沿着网格上面支路的第n 个加法器的输出，它就是假定n 阶模型之下所得的剩余量。这样就可以使E[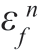（（k））2]最小，以得到参数的估计。

正如前面指出的那样，这样得到的结构产生x（k）的最佳线性均方估计，是以x（k）过去的值x（k-1），…，x（k-n）表示的。为了看出这一点，我们把估计量定义为

然后，利用正交原理，系数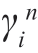 必须保证估计误差，即(www.daowen.com)

与集合x（k-j）（j=1，…，n）正交。即

有

同样，以x（k-n），…，x（k-1）写出 x（k-n-1）的估计量

则估计误差为

利用正交原理解方程组就可得到各个系数。

比较，有

得

剩余误差由如下递推公式计算，即

使E[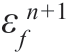（（ k））2]最小或使E[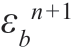（（k））2]最小，就可计算出pn+1。可以证明，pn+1 的两个估计为

和

因为x（k）是平稳的，直接计算可知，

因此，可以通过合并计算得到估计值计算式

式中的互相关系数类似于

计算。

下面简要归纳本算法。给定数据序列x0，x1，…，xL-1，可组成两个序列

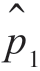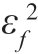计算；然后求（k）和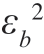（k）k=0，…，L-1；再形成所需的互相关系数并计算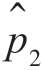。这一过程可根据需要一直迭代计算下去。

因为pn+1 仅取决于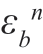（ k），很清楚，pn+1 与pj 无关，j＞n+1，这意味着与计算系数a_i 相反。当所设模型阶数增加时，不需要再计算pi。实际上，这一算法也提供了求模型阶数N 的方法。正如前面提到的，如果参数都被正确地辨识出来了，剩余的就是白噪声。因此，每一步递推运算中剩余误差的均方值为

对每个n 形成差值为

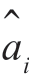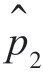如果这个量达到最小值或基本趋于一常数，则意味着进一步处理并不能减小剩余误差。这时的n 值就被认为是对应于模型的阶数。系数 可根据 算出。

Levinson 算法不需要预先确定模型的阶数N。但是，它是一种成批处理技术，并包括计算相关系数。