平稳随机过程可认为是由白噪声激励的线性时不变系统的输出。例如，对具有如下自相关序列的过程

在Z 域中的功率谱为

如果Φx（0）（1-α2）=G2，上式可改写为

于是，Φx（z）可认为是线性时不变系统输出的谱，该系统的传递函数为

它是由具有单位方差的零均值白噪声序列w（k）激励的。因此，有

其中，X（z）和W（z）分别代表x（k）和w（k）的Z 变换。

描述随机过程x（k）相应的差分方程为

类似本式定义的过程，就叫作自回归（AR）过程。于是，谱估计问题就归结为辨识该过程自回归模型参数的问题。以后，我们假定随机过程x（k）为零均值。

由于系统传递函数H（z）不具有有限零点，我们可以使模型通用化。假设H（z）为一个通用传递函数，其形式为

则系统有M 个零点和N 个极点。

令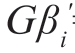=βi（i=1，…，M），则

输出X（z）为

相应的差分方程可写为

本式代表ARMA 过程。注意，如果βi=0（i=1，…，M），我们就可得到前面定义的自回归过程。如果αi=0（i=1，…，N），则x（k）为一个移动平均（MA）过程。在前一种情况下，H（z）无有限零点，为全极点函数。对于移动平均过程，H（z）代表全零点系统。

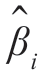设和 分别表示G、αi 和βi 的估计，定义误差为

按照估计理论相关方法，确定和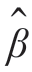，使均方误差E[ε2（k）]最小。这样得到的模型是观测数据的最佳线性均方模期。也就是说，这一模型是在均方意义上基于以往的观测和输入得出的x（k）最好的预测值。

现在我们讨论辨识ARMA 过程参数的方法。首先讨论由观测x（k）辨识自回归参数，然后把结果推广到ARMA 模型中。(www.daowen.com)

我们暂且假设βi=0，故x（k）为自回归过程。对于这种情况，差分方程变

现在可把问题叙述为，给定信号x（k）的测量值，求参数αi=0（i=1，…，N）。如果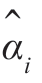代表αi 的估计，则误差为

依据均方误差最小来确定估计，即

令J 对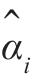的偏导数等于零，可得

即ε（k）与x（k-j）（j=1，…，N）正交。由于过程x（k）是平稳的，故将上式整理为

其中

写成矩阵形式为

该方程通常称为Yule-Walker 方程。方程左边的矩阵为托普利兹矩阵，该矩阵沿任意对角线上的元素是相同的。这样的矩阵是正定的，因此可逆。此外，估计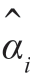将形成稳定的集，即多项式

所有零点在z 平面单位圆内，这就保证了自回归模型是稳定的。定义矩阵ΦN和向量 分别为

Yule-Walker 方程的解可写成

选择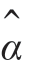得到J 的最小值为

为了计算增益G，我们注意到，如果参数已被正确辨识ε（k）=Gw（k），有

下面要确定自相关系数Φx（k）（k=1，…，N-1）。这些系数可利用

估计，其中，L 为数据序列的长度。

确定时，存在如下问题。第一，模型的阶数N 应事先已知或是固定的。第二，为了计算出相关系数，数据序列必须同时全部处理。因此，这是一种成批处理技术，它的计算既浪费存储空间，计算复杂性又高。第三，还包括矩阵ΦN 求逆。这一缺点可用三角形化过程来克服。然而，其他两个缺点仍然存在。

可用如下方法克服第一个缺点，即对各N 值计算出估计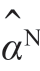，并把产生最小J值的N 作为真实模型的阶数。然而，这要求对各个N 都重复求解。下面将简要讨论这一方法——Levinson 算法。