在模式分类中，分类由特征向量来确定。如果特征的数目很大，为正确分类所需的计算量将变得很大。这就需要从给定的集合中选出少数几个特征，以便减少计算的负担，同时仍能对模式进行令人满意的分类。换句话说，需要找到能把特征向量变换成低维数的方法。一旦找到了这一问题的合理解答之后，就只需要考虑较低维数的特征向量了。所以，这个问题可看作降维问题。本节将探讨一种特征选择的方法，这种方法是基于K-L 变换的通用形式得到的。

在讨论模式分类的降维问题之前，我们先看如何选择缩维向量x（n），使之足以代表维数r ＞ n 的向量x（r）。如果x（r）的元素是不相关的，选择缩维向量的一种方法就是保留具有最大方差x（r）的分量，而舍弃其他分量。一般地，x（r）的诸分量是相关的。因此，可将x（r）用标准正交基向量g1，g2，…，gr 展开，得

其中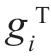， gi=δij。现要求保留展开式系数的子集〈y1，y2，…，yn〉，并仍能代表x（r）。定义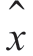（r）为

找标准正交基向量集合{gi}，使代表x（r）时所产生的均方差E[||x（r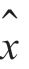）-（r）||2]为最小，即

因为yi=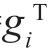 x（r），上式可重写为

其中，Vx 是向量x（r）的协方差矩阵。

所以，问题就化为使上式右端为最小，并且约束条件为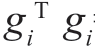，=1，可利用代价函数来解这个问题，即

其中，{λi}为拉格朗日乘子的集合。最优gi 是令梯度向量Δ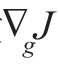 等于零而得到的，即

因此，常数{λi}是x（r）的协方差矩阵的特征值，且向量gi 是其特征向量。所以本式的展开式就是K-L 展开式的离散形式。

得到最小均方差为

因而，证明用数目少的n 个分量代表r 维的向量x（r）的最优化方法，就是将协方差矩阵中特征值按照由大到小的次序加以排列，然后，将x（r）按K-L 展开式展开，并且只保存前n 个系数。如果选一个n×r 维矩阵T，其行是Vx 的前n 个特征向量，那么降维向量x（r）则为

现在，把前面的讨论扩展到模式分类问题中的降维问题。我们将讨论限制在两类分类问题上，这类问题只要求在两种模式类别之间进行选择。给定r 维模式向量x（r），我们企图得到n 维向量x（n），而仍能在两种模式类别间进行鉴别。(www.daowen.com)

假设V1 和V2 分别为类别H1 和H2 向量的协方差矩阵，P1 和P2 为出现这两种类别的概率。定义广义协方差矩阵V 为

令D 为V 的特征向量的矩阵，则

其中，I 为单位矩阵。

如果定义矩阵Vi（i=1，2）为

就能把上式写成

令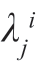和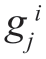分别代表Vi 的特征值和特征向量，有

则

得

本式表示，如果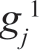 是特征值为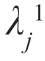 的V1 的特征向量，那么它也是特征值为1-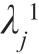的V2 的特征向量。现在若把V1 的特征值按递减次序排列，V2 的特征值则为递增次序排列。就是说，类别H1 中最重要的特征正是类别H2 中最不重要的特征，反之亦然。因此，选一个n×r 矩阵T，使其前n1 行为V1 的前n1 个特征向量，剩下的n2=n-n1 行就是V2 的特征向量。于是可得向量x（n）

其中，T=T1 D。

处理过程包括将向量x（r）展开成广义协方差矩阵V 的特征向量，并且仅保存前n1 项。同时，将n1 和n2 分别选为最接近于P1 n 和P2 n 的整数。