在实际问题中，模式类别数通常是已知的，但有时也可以是未知的。模式常用特征向量来表征，特征向量构成了分类的基础。实际上，模式的特征呈现出统计性的变量。因此，宜于将模式向量当作随机向量来看待，这种随机向量由联合概率分布函数和联合概率密度函数来描述。当这些基本分布已知并且能将受检验的模式归入已知模式类别中的一种时，问题的求解变得最简单。

通常，这些分布的形式是已知的或是可假定的，而与分布有关的某些参数可以是未知的。在这种情况下，如果其分类为已知的某些模式可用，我们就能够用这些模式样本去估计或学习分布中包含的未知参数。为学习目的而采用的具有已知分类的这些模式被当作训练样本。显然，需要学习分布函数的方法，一般不会像具有完全已知分布的模式分类方法那样来完成工作。分类方法性能好坏通常是用测定模式错误分类的概率来评价的。利用已知分类的训练样本进行学习的方式称为监督学习。

如果没有已知分类的训练样本可用，那么可以用未知分类的样本来学习或估计分类器的参数。这时，分类器称为非监督学习分类器。

上述问题可用数学形式表示。设表示模式向量，即

如果x 属M 种可能类别中第j 类Hj 的一种模式，把它表示为xj，它的诸分量表示为xij。当x 属于类别Hj 时，x 的概率密度函数表示为p（x|Hj）。如果除了某些参数θj 外，概率密度函数是已知的，则表示为p（x|Hj，θj）。(www.daowen.com)

当p（x|Hj）（j=1，2，…，M）为已知，并且检验模式x 已分入M 种类别中的一类时，问题最简单。判决规则（鉴别函数）可以是线性的、平方律的或由p（x|Hj）决定的其他形式。

监督学习模式分类问题可表述为，对于每类情况，或者知道密度函数p（x|Hj），或者知道条件密度函数p（x|Hj，θj），其中，θj 表示未知参数的向量。对于参数θj 对应的每种类别，我们给出属于这一类别的训练模式集合ZNj=[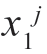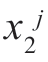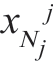，，…，]。我们可以假定参数θj 或为确定型变量或为随机变量。在后一种情况下，我们要设定一个参数的先验概率密度函数，然后得到一种判决规则来对检验模式x 进行分类。机器主要工作于两种方式。学习方式利用已知分类的样本来估计未知参数；检验方式则根据学习方式结束时形成的判决规则来把新的样本分入各种不同的类别。

在非监督学习中，给定一组分类未知的模式集，ZN=[x1，x2，…，xN]。对于具有未知参数的类别，学习向量θj 必须用这些未分类的样本进行处理。对出现的任何新模式，也可以用来改善对未知参数的估计。在这种情况下，学习和检验方式之间并没有明显的差别。但是，对于非监督学习，所需的计算量和存储量随着样本模式的增加会变得非常大。

我们从已知概率密度函数的分类问题开始讨论。为清楚起见，我们把大多数讨论限定在只有两种模式类别的情况，其结论很容易推广到M 种类别的分类问题。