非约束的图像复原方法多建立在线性系统的基础上，如图8-5 所示。

图8-5　图像复原的去卷积滤波方法

首先我们假定图像退化中的噪声可忽略不计，根据卷积定理，由退化模型得

从而有

令退化图像g（x，y）通过一个传递函数为

的线性滤波器就可复原图像f（x，y）。这一方法常称为“逆滤波”（Inverse Filtering）或“去卷积”（Deconvolution）。

这种看起来简单易行的方案，实际上没有实用意义。因为hd（x，y），在某些频率上可为零，即使逆滤波器存在，也会由于hd（x，y）的低通性质，使其在高频区域幅值很大，从而造成原本可忽略的微弱噪声被放大。下面采用维纳滤波器。

维纳去卷积滤波理论的出发点是使复原图像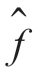（x，y）与原始图像f（x，y）的均方误差达到最小，即使下面的方差最小化(www.daowen.com)

其中，hr（x，y）是图像复原传递函数；hd（x，y）是图像退化函数。

在原始图像f（x，y）和n（x，y）噪声均为平稳随机过程，且其中之…的均值为零的条件下，可对复原函数hr（x，y）求导等于零可得到

其中，Rf（τ）和Rn（τ）分别是原始图像f（x，y）和n（x，y）噪声的自相关函数。傅里叶变换后可得

其中，Pf（u，v）和N（u，v）分别为f（x，y）和n（x，y）的功率谱。在白噪声情况下，N（u，v）为常数。

一般地，我们没有关于Pf（u，v）的先验知识。在具体图像复原设计时还必须做进一步假定。可知，维纳去卷积滤波器Hr（u，v）可看成两个滤波器的级联。其中，前一滤波器就是前面提到的逆滤波器，而后一滤波器的传递函数为

称为维纳滤波器。