利用图像的统计特征可以有效地实现图像压缩。基于统计特征的图像编码根据图像的统计特征，可用较少的比特数表示出现概率较大的灰度级，而用较多的比特数表示出现概率较小的灰度级。

设一幅数字图像第i 级灰度编码所用的码字长度为βi 比特，其相应出现的概率为Pi，那么，可以定义该N 级灰度数字图像的平均灰度码字长度即

进一步定义编码效率，即

其中，H 为该数字图像的信源熵，即去除冗余后的信息量；L 为平均灰度码字长度。

根据统计编码理论，可以证明，只要使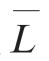等于或接近H，这种图像压缩的编码方法称为最佳编码。这种最佳编码要求在编码过程中不丢失信息量，即要求保存信息熵，这种信息保持编码又叫作熵保存编码，或者叫熵编码。熵编码的特点是无失真数据压缩，这种编码经解码后可无失真地恢复原图像。下面介绍的霍夫曼编码（Huffman Coding）和香农编码（Shannon Coding）即属于摘编码。但是若编码结果使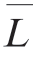＜H，则必然会丢失信息。

（一）霍夫曼编码

霍夫曼编码是根据可变长最佳编码定理，应用霍夫曼算法而产生的一种编码方法。对于出现概率大的信息符号编以短字长的码，对于出现概率小的信息符号编以长字长的码，如果码字长度严格按照符号出现概率大小的相反顺序排列，则平均码字长度一定小于按任何其他符号顺序排列方式的平均码字长度。霍夫曼编码已被证明具有最优变长码性质，平均码长最短，接近熵值，而且是一种无损压缩编码。

设信源X 有m 种不同符号（对于图像就是灰度级），对应的符号和出现概率为

霍夫曼编码的步骤如下。

1.先将信源X 中的不同种类符号按概率从大到小顺序排列（对于概率相同的可任意排列位置）。

2.把最后两个出现概率最小的两个符号类别合并成一个符号类别，从而使信源的符号类别数减少，重新按信源符号类别出现的概率从大到小排列。(www.daowen.com)

3.重复上述两步骤，直到信源最后为两个符号类别为止。

4.将被合并的符号类别分别赋予1 和0，并对最后的两个符号类别也相应地赋予1 和0。通过上述步骤就可构成最优变长码。

（二）香农编码

香农编码也是一种常见的变长编码，利用该编码有时效率可达到100%。香农编码的步骤如下。

1.统计每个灰度出现的频率。

2.从上到下将灰度按其出现的频率降序排列。

3.从序列中的某个位置将序列分成两个子序列，并尽量使两个子序列的频率和近似相等。给前面一个子序列赋值为0，后面一个子序列赋值为1。

4.对子序列重复步骤3，直到各个子序列不能再分。

5.将每个元素所属序列的值串起来，这样就得到了各个元素的香农编码。