K-L 变换简单地说就是将N 维随机变量变换为M 维主分量的线性组合，且M＜N，变换后的系数能量主要集中在少数主分量上，使信息能量集中，便于数据压缩和模式识别。

（一）连续随机信号的K-L 展开

连续随机信号的K-L 展开是指定义在时间区间[0，T]上的随机信号x（t）可以用基函数Φi （t）（t=1，2，…）的线性组合来表示，即

其中，{Φi（t）}是完备正交基，满足正交归一化条件，即

系数yi 又是随机变量，定义为40 在Φi（t）分量上的系数，即

同时，{Φi（t）}是由x（t）的统计特征得到的正交基。设x（t）的期望E[x（t）]=0，将x（t）的协方差函数定义为

满足yi 互不相关即 的特征方程为

其中，Φi（t）是以协方差函数为核的积分方程的特征函数；λi 为积分方程的特征值。

（二）数字图像的K-L 变换

设某幅M×N 大小的图像f（x，y），经某个传输通道传输了P 次，由于受到各种因素的随机干扰，接收到的是一个图像集合，表示为

将每幅图像Xi ∈RM×N 表示成一个向量，它是一个M×N 维的随机向量，即

将P 次传输的图像集合写成P 个M×N 维向量{X1，X2，…，XP}。数字图像的K-L 变换就是，选取一个合适的正交变换A ∈RL×M×N 使得变换后的图像Y=AX 满足下面两个条件。

1. Y 是具有L ＜＜M×N 个分量的向量，即维数降低或信息能量集中。

2.由Y 经反变换而恢复的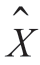（向量X 的近似值）与原始图像具有最小的均方误差，即

数字图像的K-L 变换意味着不仅删除了M×N-L 个分量，而且由变换结果Y重新恢复的图像是有效过滤随机干扰的原图像的最佳逼近。(www.daowen.com)

（三）数字图像K-L 变换的具体实现

K-L 变换可以理解为已知N 个点（xi1，xi2）（i =1，2，…，N）的二值数字图像，先对这N 个点求出第一条“最佳”拟合直线，使得这N 个点到该直线的垂直距离的平方和最小，此直线就是第一主成分；然后求与第一主成分相互独立（或者说垂直）且与这N 个点的垂直距离平方和最小的第二主成分。依此类推，可得到多个主成分。

对于一幅M×N 大小的灰度图像，将其看作M×N 维的随机向量。其协方差CX 可按公式求得，式中模式向量的均值按多幅图像的统计均值近似替代。

设λi 和ei 是协方差矩阵CX 对应的特征值和特征向量，其中，i=1，2，…，M×N。将特征值按递减排列，即λ1 ＞λ2 ＞λ3 ＞…＞λM×N，则K-L 变换核矩阵A的行由CX 的特征向量构成，即

其中，eij 表示CX 的第i 个特征向量的第j 个分量。A 为（M×N）×（M×N）的方阵。

数字图像K-L 变换可以表示为

其中，X-MX 为原始图像X 减去平均值向量MX，称为中心化图像向量。数字图像的K-L 变换是中心化图像X-MX 与变换核矩阵A 相乘所得的结果。

K-L 变换后得到的各向量间是无关的，其协方差矩阵为

通过逆变换可以由较少的数据重构图像X。得

由于矩阵A 的各行都是正交归一化矢量，所以

无损变换是取全部特征向量构建变换矩阵A。若只取k 个较大特征值对应的特征向量构造Ak（k ＜＜M×N），则

此时，重建均方误差为

因此，K-L 变换是在均方误差最小意义上的最优变换，去相关性好，可以用于数据压缩、图像旋转和特征分析。但K-L 变换也具有明显的缺点，即二维K-L变换不是可分离的变换，不能通过在x 和y 方向上的两次一维K-L 变换来完成二维K-L 变换的运算。同时，K-L 变换是一种与图像数据有关的变换，变换中必须计算大小为（M×N）×（M×N）的协方差矩阵的特征值和特征向量，计算量非常大。