现在讨论雷达目标的状态估计问题。假定雷达目标做匀速或匀加速直线运动，同时，考虑动态噪声ω（t）的扰动和观测噪声n（t）的影响。通常情况下，目标的距离比较容易获得，所以，一般通过距离测量来估计目标的状态。

（一）匀速直线运动目标状态的估计

如果雷达目标做匀速直线运动，并且受到一个机动加速度的扰动，结果每一次观测引入一个随机的增量。在这种情况下，为了得到目标的离散状态方程，先分别写出目标的距离方程和速度方程，即

和

其中，rk 和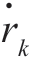 分别表示目标在第k 时刻的距离和速度；T 为相邻两次观测的时间间隔：vk-1 是由机动加速度在一个观测周期内引入的随机速度增量。

由目标的距离方程和速度方程，我们可以得到h 时刻目标的离散状态方程，即

其中

如果雷达观测中存在观测噪声，于是，第k 时刻的雷达观测方程为

其中，H 是观测矩阵；nk 是观测噪声。

现在假定目标初始状态的统计特性为(www.daowen.com)

{ωk-1}和{nk}分别是零均值白噪声序列，且

目标起始状态x0 与随机噪声序列{ωk-1}和{nk}都不相关。

这样，在获得观测值zi（i =1，2，…k…）后，应用卡尔曼滤波公式，就可以对目标的状态（距离和速度）进行估计和预测，得到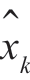 和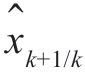。应当说明，如果动态噪声序列{ωk}和观测噪声序列{nk}各自是相关的，则可按照噪声时的卡尔曼滤波处理方法来处理。

（二）匀加速直线运动目标状态的估计

在匀加速直线运动目标情况下，如果目标受到随机动态噪声的扰动，使得在每一个观测周期内引入一个随机加速度增量x0。于是，第k 时刻目标运动的离散状态方程为

其中

雷达在第k 时刻的观测方程为

其中，H 是观测方程；nk 是观测噪声。

假定目标的起始状态为x0，随机加速度增量序列{ωk}和观测噪声序列{nk}的统计特性和相关性与匀速直线运动的情况相同。这样，在获得观测值{Zk}后，利用卡尔曼滤波公式就可以对目标的状态（距离、速度和加速度）进行估计和预测了，这与匀速直线运动的情况相似。