信道均衡是对传输特性不理想所造成的传输信号线性失真的补偿和修正。信道均衡分为频率域均衡和时间域均衡。随着数字通信的发展，时间域均衡得到广泛应用。失真的传输信号经过时间域均衡器后，在各抽样点上的总符号间干扰极小。常用的时间域均衡器是自适应时间域均衡器，它能随时追踪信道特性的变化，保持最佳的工作状态。迄今为止，讨论时都假定信道的冲激响应h（t）或它的采样值hn 是已知的。但在实际中这只能是近似成立的，因为信道的特性可能是随时间变化的。许多情况下，采样值hn 可能是未知的。这时，设计均衡器必须依靠某种自适应技术直接或间接地辨别采样值hn，同时起均衡作用。

一般地，理想均衡器是使均衡后的系统（即信道与均衡器级联）可以表示为纯增益（或纯延时）。若用{hk}表示均衡系统的加权序列，则必有

Lucky 提出的均衡器是一个可变抽头的延时线性滤波器，调节抽头增益使被均衡系统的加权序列近似为本式所示的hk。由于信道的特性经常改变，隔一段时间就必须重新调整抽头增益。为了求出周期性调节抽头增益的算法，假定信道特性变化得较慢，在M 个观测间隔内可以假设它是固定的，如图7-22 所示。若用an 表示发送的序列，接收机处（均衡器输出端）的观测模型为

图7-22　自适应均衡器方案

假定式中的噪声取样vk 是独立同分布的高斯随机变量，均值为零、方差为σ2。同时，假设均衡信道的冲激响应完全可用2N+1 个取样表示。要在任意M 个信号间隔上指出加权序列{hk}（k=-N，-N+1，…，N-1，N）的最大似然估计量。为了方便起见，定义2N+1 维向量H 和M 维向量Z 分别为

根据上述假定，不难写出条件概率密度p（z|h）为

对数似然函数为

令（∂lnp（z|h）/∂hj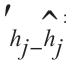）=0，得到包含2 N+1 个方程的联立方程组，解此方程组就可以求出2N+1 个响应值hj（j=-N，-N+1，…，N-1，N）的最大似然估计。因此

或

本式是一个线性联立代数方程组，解此方程组可以求得估计量。假定发射的各种符号是独立的，则此方程组可以简化。此时，对于充分大的M，有

其中，S 表示发送序列的平均功率。这时，估计量为(www.daowen.com)

现在调节均衡器抽头增益的算法变得很简单了。为了实现理想均衡，要求h0=1 且n ≠0 时，hn=1。因此，n=0 时，若hn 为正，则减少抽头增益某一固定量；若hn 为负，则把抽头增益增加。该自适应均衡的方案如图7-23 所示。计算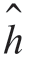要求在接收机处可以得到发送序列。如果错误概率很小，则检测器的输出 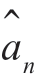可以用来代替式中的an。

理想情况下，h0=1 且n ≠0 时，hn=1。因此，n ≠0 时估计量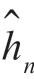 应很小。为了得到适当收敛的估计量，观测量的数目K 必须相当大。为了解决这个问题，可以不去估计h0 本身，而是去估计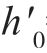=h0-1。定义n ≠0 时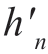=hn，则估计量 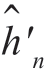在所有n 值，其大小的数量级相同。利用 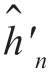容易写出似然函数为

因此，最大似然估计量为

图7-23　自适应均衡器结构

其中

不难确定估计量的矩，有

其中，最后一步，根据序列{ak}的独立性推出来的估计量是无偏的。估计量的方差为

经过大量的代数运算，可以化为

对均衡器的精度和建立时间来说，更重要的一个量就是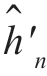 与hn 符号相同的概率，记作pc。M 较大时，由于 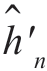是均值为hn 的高斯变量，所以，不难看出|hn|大时pc=1，而当|hn|较小时pc=0.5。后一种情况下，抽头增益是“游动”的，因为增益调节算法的校正作用具有振荡性质，通常设计自适应均衡器时都要求保持抽头增益“游动”在一定范围以内，范围的大小由精度要求决定。上式可以当作一个设计关系式，用它可以计算出给定任何N 值时所要求的M 值。