到目前为止，只讨论了数字通信系统中产生错误的两种来源，即加性噪声和传输媒质上的衰落。讨论过程中做了一个重要的假定，即信道无任何记忆能力，从而各个信号间隔上接收的信号可以认为是与其他间隔上的信号独立无关。但是，这样的假定在高速数据传输情况下是不成立的。例如，计算机之间的通信，任何一个信号间隔上接收的信号都受其他几个间隔传输信号的影响。由于传输的信号被弄模糊，对判决过程产生有害的影响。这种现象一般称为符号间干扰（ISI）。

本节阐述具有符号间干扰的基本数字通信系统的模型，计算检测数字时错误概率的增加量。为了应对这些影响，可以先把观测到的信号通过一个叫作均衡器的滤波器，均衡器的特性正好与信道特性相反。如果均衡器严格地同信道匹配，则信道与均衡器合在一起正好是一个纯增益，使均衡器的输出不出现符号间干扰。下面仅限于讨论依数位逐个检测情况，但许多结论可以推广到数码序列情况。维特比（Viterbi）提出了一种算法，解决这个问题很有成效。

为了解释有关的各种概念，我们仅以基带系统为例进行研究，其结果原则上可以推广到其他调制系统。令{an}（n=-∞，…，-2，-1，…，∞）是以等概率取值+1 或-1 的二元白色序列。可以把这个序列看成图7-18 所示二元基带数字通信系统输入数码的一种表示。其中，h（t）代表信道冲激响应，v（t）是加性噪声。为了便于分析，把输入看成权值为的冲激序列。这时可以每隔an 秒把接收信号同步地取样一次，以判决发送的数码是1 还是-1。由此得接收信号为

图7-18　具有符号间干扰的基带数字通信系统

考察某一取样瞬间如t0，它对应于传输a0。这个取样可以表示为

其中，h0 代表h（t0）；h-n 代表 h（t0-nT）；∑ 表示不包括a0 项的求和。本式清楚地体现了信道记忆和加性噪声的影响。第一项相当于要求的信号；第二项是信道记忆作用造成的，它表示符号间的干扰效应，最后一项是加性噪声。即使没有加性噪声（这种情况是罕见的），第二项也是很严重的，它足以引起错误的判决。因此，我们看到在有记忆信道上做高速数据传输时符号间干扰是错误的主要来源。为了使系统可靠地工作，就要减小它的影响。考察一下上式，可以注意到一种有意义的问题，这就是符号间干扰项是相关的随机序列，可以把这个检测问题看成非白噪声中的已知信号检测问题。“最佳”接收机的结构是白化滤波器加上适当的匹配滤波器。但是，设计这样一个接收机，在实际中要受到多方面的限制。为了得到使符号间干扰作用最小的设计方案，还需要借助某些近似公式。

有非白噪声存在时，接收机的性能依赖于发送信号的波形。因此，只要恰当地设计发送信号的波形，就能减少错误概率。由于可以把符号间干扰看成非白噪声，可以用这种方法获得好处。如果我们能计算与非白噪声过程nT））最小特征值对应的特征函数，并且用它来传送：元数据，检测能力确实可以提高。但在实际中这个计算相当困难，甚至最后可能算出一种极为复杂的波形，根本不能实现。因此，通常都不用上面考虑的这种波形，而是设计一种在取样瞬间响应为0 的波形，如升余弦波形。

现在讨论减少符号间干扰效应的均衡器设计问题。设计均衡器的一种准则是使如下定义的峰畸变Dp 最小，即

此外，也可使均方畸变Dms 最小，即

实际中可以假定信道的记忆时间是有限的。因此，本式中的无限和可以用有限和来代替。均衡器选择为具有L 个抽头的抽头延时线，并且调节每个抽头处的权值，使Dp 或Dms 最小。

接收机有加性噪声时，可以选均衡器抽头使输入序列与均衡器输出间的均方误差最小。图7-19 画出了这种方案的主要组成部分。

图7-19　加了均衡的数字通信系统

于是，给定观测值后

问题就是设计均衡器的增益Cl（l=-L，-L+1，…，0，…，L），使得均衡器输出为(www.daowen.com)

在均方意义下近似于发送的符号an-D。大多数情况可选L 等于W。如果用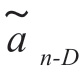表示估计误差，则可用正交投影原理，得

其中

可得

本式右边是延时的输入与尚未达到均衡信道输出（观测量）之间的互相关，而左边的数学期望对比于尚未达到均衡信道输出的自相关函数。于是，有

其中，最后一步是根据假定发射信号的独立性推得的。类似地，可以证明

得

本式构成了含有2 L+1 个方程的联立代数方程组，解这个方程组就可以求出最佳的抽头增益{cl}。在没有加性白噪声时，可以证明，最小均方估计法与均方畸变最小法相同。

使用卡尔曼滤波器，可得到均衡器设计的序列解。假定这时信道模型与上式相同，但干扰是单边的，即只有来自过去已发送符号的干扰。这时，h-n=0（n=1，2，…，N）。图7-20 画出了信道模型。延时线的输入是一串二元独立随机数字u（k）且u（k）=ak，输出受到平稳加性白色噪声v（k）干扰，v（k）的方差为vc。假定u（k）和v（k）在所有时刻都是独立的。根据图7-20 可推得信道的动态方程，并可用状态变量表示为

其中，x（k）是n 维状态向广向量；u（k）是标量输入；z（k）为受噪声干扰的输出。矩阵F、向量G 和H 分别为

现在的问题是求随机的均衡算法，条件是已知输入统计特性和噪声统计特性，由此二者可在某一延时后的时刻k+ D（0 ≤ D ≤ N-1）得到消息u（k）的估计量。

在任一时刻k，都有观测记录z（k）={z（j），j ＜k}，所以，上述问题可以重新表述为根据这些测量结果，随机估计x（k）的第D+1 个分量问题，即估计x1+D（k）= u（k-D）。可以用卡尔曼滤波器算法得到状态向量x（k）的最小方差估计，它给出了本问题的直接解。根据均衡器（卡尔曼滤波器）的结构，如图7-21 所示。有关均衡器结构和方程的详细推导留作习题。应当指出，这种均衡器的优点是，对所有0 ≤ D ≤ N-1 条件下的估计量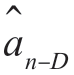是同时得到的。

图7-20　卡尔曼均衡器的符号间干扰信道模型

图7-21　符号间干扰信道的卡尔曼滤波器框图