相干通信系统为了有效工作，要求有不同程度的同步，在已知信号波形的基带传输系统中，接收机必须知道信号出现的开始和终止时间。对于射频通信系统来说，还必须知道载频的相位。此外，若把数字组成字，还必须知道字出现的起始和终止时间。

首先研究载波的同步问题。如果发送信号中包含载频分量，只要锁定这个分量，就可以很简单地得到载频的相干。实现锁定最通用的装置通常采用图7-15 所示的锁相环路（PLL）。该系统包括相位检波器、环路滤波器、环路放大器和压控振荡器（VCO）。为了了解锁相环路的工作原理，假定输入信号为

图7-15　锁相环路框图

压控振荡器的输出为

相位检波器的种类很多，假定我们采用乘法器后接低通滤波器，滤波器的作用是消除乘法器输出的二次谐波项。因此，相位检波器的输出为

其中，Kd 是与乘法器有关的常数。压控振荡器实际上是一个调频器，它的输出频偏dΦ（t）/dt 正比于加到压控振荡器输入的电压ev（t），于是

其中，Kv 是压控振荡器常数。假定锁相环路中的环路滤波器和环路放大器可以用某一增益代替，则可解得

显然，根据上式，当θ（t）＞Φ（t）时，dΦ（t）/dt 是正的，Φ（t）将增加；类似地，当θ（t）＜Φ（t）时，dΦ（t）/dt 是负的，Φ（t）将减少。在这两种情况下，Φ（t）相对于θ（t）的变化方向总是使得最后θ（t）= Φ（t），从而实现锁定。于是，压控振荡器的相位Φ（t）是载波相位θ（t）的一个很好的估计。还可看出，如果θ（t）和Φ（t）之差大于π/2，压控振荡器就跟不上载波相位。有关锁相环路的详细分析已超出本书的范围。

发送信号没有载波分量时（如PRK 情况），可以采用柯斯达斯（Costas）同步环路。图7-16 画出了柯斯达斯环路的方框图。假定输入信号yr=Ercos ωc t 时，图中标出了环路中各点的信号。压控振荡器前低通滤波器的输出实际上是其输入的直流值。这个信号控制压控振荡器，最后使外θ（t）变为零，从而实现相位锁定。

图7-16　柯斯达斯环路

数字同步一般包括3 种方法。例如，让发射机和接收机跟随同一时钟引入同步，也可以使用单独的同步信号（主控时钟），还可以根据本身的调制实现自同步。此外还可用最大后验估计法来估计这个定时偏差。现以二元PRK 系统为例解释一下。假定发送信号是

假定只y1（t）和y0（t）是等概率的，令θ 表示定时偏差，接收信号的模型是

其中，v（t）是平稳的白高斯过程，均值为零，方差为N0/2。(www.daowen.com)

使用类似的方法求数位偏移的估计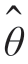。为了求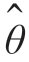 map，在任一数字间隔上用正交基函数集{gk（t）}把z（t）展开，令zk（t）表示z（t）的N 项近似，即

其中

不难推知，系数{zk}是独立的高斯随机变量，它们的矩量为

根据本式，有

然后，可以写出zk（t）以θ 为条件的概率密度函数，即

由于已假定“1”和“0”信号是等概率的，并且在每种假设下，{zk}都是独立高斯随机变量集，均值和方差由本式给定，所以

同时

假定θ 在[0，T]上均匀分布，上式的分母正好是归一化因子。所以，当K 趋于无穷时，上式右端的表示式最大，就可以求出θ 的最大后验估计。于是，有

其中，E 表示已调信号的能量。此外

由于coshx 是x 的非减函数，得

假定θ 在区间[0，T]上只取L 个离散值，则可得到它的实际实现方案。这时，对L 值中的每一个值都进行一次计算，然后选其中最大者为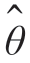 map 值。图7-17 画出了这种估计器的结构。

图7-17　估计单个间隔h 数位偏移的最大后验估计器