本节介绍二进制调制系统在满足最佳接收准则下的3 种最佳接收机，即匹配滤波器接收机、相关接收机及理想接收机。对其各自性能进行推导及相互比较，并将理想接收机与实际接收机进行比较。

1.最佳接收机不是一个绝对的概念，在某个准则意义下的最佳接收机，在另一个准则下则并非最佳。数字通信中常用的最佳准则有最大输出信噪比准则、最小均方误差准则、最大后验概率准则等。

2.匹配滤波接收机是在最大输出信噪比准则下的最佳接收机。匹配滤波接收机是由两个匹配滤波器和判决器组成。匹配滤波器的幅度特性与信号的振幅特性相同，而相位特性与信号的相位特性相反。同时，匹配滤波器是输入信号与噪声的互相关器，是输入信号的自相关器。正是由于匹配滤波器的这种特性，其输出信噪比得以很大提高，有利于信号取样判决，减小误码率。

3.最小均方误差接收机是在最小均方误差准则下的最佳接收机。它由两个相减器、两个平方器、两个积分器和判决器组成。由于结构复杂不易实现，故常用相关器实现。相关接收机是由两个乘法器、两个积分器和判决器组成。乘法器和积分器合称为互相关器。

4.理想接收机是按照最大后验概率准则建立起来的最佳接收机。后验概率也可用似然函数表示。所以，最大似然函数准则与最大后验概率准则是一致的。

5.对于3 种准则下建立起来的3 种最佳接收机，可以证明，在高斯白噪声信道内，它们的接收性能是等效的。但对于非高斯型信道，则接收性能不一定等效。

木节讨论一些基本的数字通信方案，推导相应的接收机结构。我们仅限于讨论二元信道，即该信道对应的信号仅由符号0 或1 组成。因此，编码器的输出应是1 和0 构成的序列，序列中每个符号的出现速率是每T 秒一个。与0 对应的信号是y0 （t），与1 对应的信号是y1 （t）。

直接传输波形y0 （t）和y1 （t）的基带传输方案通常较少使用，所以，本节讨论射频数字通信的最佳接收机。前面已经提到，远距离通信时波形要去调制一个高频载波。这种情况下，在解调用的接收机中，如果有一个与发送载波相位同步的本地参考信号，那么该系统就称为相干的，否则称为非相干的。类似地，如果在接收机中有一个与所发送的脉冲序列同步的周期信号（称为时钟信号），该系统就称为同步的；如果得不到这样的时钟信号，则称该系统为非同步的。

远距离数据传输系统很少采用基带传输。通常是用数字数据去调制一个正弦载波。为了保持一定的信噪声比，沿途隔一定距离还设置了中继器。基本的数字调制方式有幅移键控（ASK）、频移键控（FSK）和相移键控（PSK）。在二元信号情况下，幅移键控采取的方式是发送载波代表1，不发送载波代表0，因此，称为启闭键控（OOK）。

本节将推导上述各种情况下的最佳接收机结构及其性能；考虑其中某些接收机在衰落媒质中的工作情况，指明改善这些接收机性能的方法。首先根据二元通信的相关接收机，得出下面要研究的相下检测系统。

相干系统的接收机有一个与发射载波相位同步的本地参考信号。由于载波相位已知，为了便于分析相干系统，可以假设载波相位等于零而不失一般性。下面着手分析各种不同方案。

启闭键控系统，在T 秒间隔内用叫代表“传号”信号（数字1），用y0（t）=0 代表“空号”信号（数字0）。假定接收信号z（t）是由发射信号yi（t）（i=0，1）和干扰信号组成，其中，干扰信号是功率谱密度为N0/2 的加性白高斯噪声。最佳接收机如图7-10 所示。

图7-10　启闭键控系统的最佳接收机

“传号”和“空号”出现的概率相等，采用最小错误概率准则时，可以得到门限为E/2，这种情况与单极性基带传输类似。此外，每个数字的平均能量为E/2，信噪比为N0/E。由于相关系数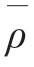等于零，可以求得错误概率为

图7-10 所示的接收机可用一个乘法器（混频器）后面接一个低通滤波器来实现，也可以用一个中心频率为ωc 的带通滤波器来实现。

频移键控系统（FSK）采用

代表数字“1”，用

代表数字“0”。通常载波频率这样选择，使在间隔T 内每个信号以及它们的差拍信号都有整数周期。这种情况下，相关系数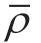为

因此两个信号是正交的。这种数字传输系统称为正交FSK 系统。平均能量是

接收信号z（t）是y0（t）或y1（t）受到谱密度为N0/2 的白噪声加性干扰后得到的。最佳接收机的结构如图7-11 所示，包括两个相关结果的差同门限的比较。实际实现时，相关器还可用混频器后接一个低通滤波器来代替，或是用两个相应中心频率的带通滤波器来代替。错误概率可以根据基带数字通信的公式直接求出，即

图7-11　最佳相干FSK 系统

对于FSK 系统来说，每个数字的平均能量与噪声谱密度之比为2 E/N0，而OOK 系统则为E/N0。因此，每个数字的平均能量与噪声谱密度之比相同时，相干OOK 系统与正交FSK 系统具有同样的性能。但由于正交FSK 系统在衰落信道上的性能较好，所以，实际中倾向采用正交FSK 系统。

相移键控（PSK）情况下，“1”和“0”信号分别用和表示。这种系统也称为反相键控（PRK）系统。由于相关系数等于-1，这种系统是一种理想系统，平均信号能量为E。当加入谱密度为N0/2 的加性白噪声时，最佳接收机如图7-12 所示。

图7-12　PSK 系统的最佳接收机

出于PSK 系统本身的特殊性质，它必然是相干的。因为载波相位若是完全随机，它就不可能传送信息。根据基带数字通信公式，不难得到错误概率，即

可知，对于给定的容许错误概率来说，PRK 系统要求的每个数位平均能量比PSK 系统低3dB。如果要实现相干系统，显然应该选用PRK 系统。

在非相干系统中，接收端得不到载波的相位。可以预料，非相干系统与相应的相干系统比较，性能将会变差。但由于它比较简单，所以，很多应用场合仍然广泛地采用非相干系统。

在非相干OOK 系统中，在每T 秒的间隔内，简单二元假设下接收信号分别为

其中，θ 是非相干系统中一个未知参数。我们仍假定加性噪声是谱密度为N0/2、均值为零的高斯噪声。

如果θ 是一个已知概率密度为p（θ）函数的随机变量，可以先求条件似然比Λ（z|θ），然后对己知的概率密度p（θ）进行积分求平均，得到似然比Λ（z），即

由此不难推得条件似然比为

定义

容易证明，在二元假设下，Ls 和Lc 都是高斯随机变量，现在假定θ 在[-π，π]中均匀分布，可以推得用Ls 和Lc 表示的似然比为(www.daowen.com)

其中，I0（·）是第一类修正贝塞尔函数。当出现“1”和“0”的概率相等时，判决规则为

其中，γ′为门限值。当x 值较小时，ln（I0（x））=x2/4；而当x 值较大时，ln（I0（x））=x。因此，无论高信噪比还是低信噪比，判决规则都近似为

它可以采用带通滤波器与包络检波器级联来实现。图7-13 画出了接收机的结构；新的门限值按所用的近似式计算得到；（是一个充分统计量。

图7-13　非相干OOK 接收机

为了计算错误概率，还需要知道p（l|H0）和p（l|H1）。由于Ls 和Lc 都是高斯随机变量，容易推得

和

当发送信号“1”时，错误概率为

其中，Q（a，b）为马库姆（Marcum）Q 函数，即

类似地，发送“0”信号时的错误概率为

因此，总的错误概率为

为使错误概率最小，必须根据因子2 E/N0 来选择门限γ。令式（7-2-19）中的pe 对γ 偏导数为零，就可以得到最佳门限。于是得到超越方程，即

根据此式可以解出归一化门限（2 /N0） 1/2 γ。得到一个极好的解析近似解为

上式所示的错误概率表达式相当复杂。但是，信噪比E/N0 比较高时，对于较大a 和b 值有

可以得到pe 的近似表达式。代入公式得

信噪比较大时，推得最佳门限值满足

当x 很大时，可用erfc*[x]近似，即

得高信噪比情况下，非相干00K 系统的错误概率，即

由此可见，信噪比上升时误码率指数下降。应当指出，对于给定的错误概率和噪声谱密度，最佳非相干OOK 系统比相干OOK 系统要求的信号平均能量多1dB。

对于二元非相干频移键控系统来说，在二元假设下，接收信号为

通常，频率ω1 和ω2 相隔很远。对于这种情况，引进一个“零假设”（没有信号）作为虚假设，再遵照非相干OOK 情况，就不难推导出最佳接收机。

假定相位在（-π，π）上均匀分布，则可以用两个中心频率分别是“1”和“0”信号频率的带通滤波器、包络检波器实现最佳接收机。每一个信息脉冲间隔（T秒）比较一次包络，并根据包络较大者做出判决。图7-14 画出了非相干FSK 接收机结构框图。

图7-14　非相干FSK 接收机框图

设“1”和“0”信号是等能量的正交信号。为了推导接收机的性能，假定发送了一个“1”信号y1（t）。图7-6 上方的检波器输出代表“1”信号加噪声后的包络v1，下方的检波器输出只是噪声包络v0。当发现“1”信号而v0 超过v1 时就出现一次错误，令Pe1 表示错误概率。可得到概率密度函数p（v1|H0）和p（v0|H1）的表示式，即

因此

利用Q 函数的积分关系式，得

类似地，可以得

因此，总错误概率为

对于给定的E/N0，非相干FSK 的性能要比非相干OOK 好，因为FSK 系统用了两倍的能量。因此，给定每个数字平均能量与噪声功率的密度之比，非相干FSK 与OOK 的性能几乎相同，该比值比较低时的情况例外。

可以得到大信噪比条件下非相干FSK 系统和相干FSK 系统性能的比较关系式，即

信噪比高时，相干FSK 的性能比非相干FSK 的性能好。但是，随着信噪比增大，由于PS 的变化主要受指数项支配，两者性能之间的差别很小，可以忽略。

实际中，非相干FSK 使用比较广泛，主要原因为：① 结构简单：② 门限与E/N0 比值无关；③ 高信噪比时，性能抵得上相干FSK；④ 衰落信道中的性能比非相干OOK 好。