观测模型如下

其中，v（t）是零均值高斯随机过程，它的谱密度为N0/2。各种调幅信号y（x（t），t）为双边带调幅，即

双边带抑制载波调幅为

残留边带调幅为

以上情况都假定消息的频带远小于载波频率。

对于双边带调幅和双边带抑制载频调幅，最大后验方程均由上式给出。此时，

因此，估计方程为

假定x（t）是平稳过程，并且假定-∞＜ t ＜∞，即可推得该方程的解。此时，可得

由图7-3 可推得这个估计器的方框图，如图7-4 所示。环路滤波器相对于载频来说是一个低通滤波器。对应于的倍频项将被环路滤波器过滤。(www.daowen.com)

图7-4　最大后验的调幅接收机结构

可得

忽略倍频项，可以得到如图7-5（a）所示的结构。如果用一个滤波器代替反馈环路，就可导出图7-5（b）所示的系统。估计量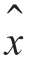（ t）是根据整个区间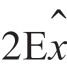（ t）sin2ωct上的观测量集合做出的估计。因此，最佳解调器由乘法器和一个不可实现的最佳滤波器组成。可以把估计量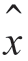（t）想象成无限滞后的平滑滤波器的输出。因此，这个非因果滤波器可以用一个可实现滤波器和无限延时来代替，利用足够长的延时可以得到实际的结构。

图7-5　幅度调幅的另一种结构

在残留边带调幅情况下，解调器的有关表示式做一些代数变换，可以证明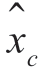（t）和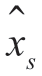（t）分别为

对于单边带调幅情况时，上述公式会变得非常简单。

双边带调幅和残留边带调幅系统，由于载频未被抑制掉，要比双边带抑制载波调幅或单边带抑制载波调幅系统有较大的估计误差。因为可用功率有一部分消耗在发送载波上。但这些系统的优点是接收机容易得到载波。因为求解调器的结构时假定接收机端的载波是确知的。对于抑制载波的系统来说，接收机必须根据混有噪声的发送信号观测波形来恢复载波。例如，设置一个导频可以帮助恢复载波。无论如何，由于信道有噪声，接收机的性能有可能因此而显著恶化。