信号波形估计问题，在求模拟通信系统接收机结构的过程中起着非常重要的作用，该系统待发射的信号以线性或非线性的方式调制载波，调制的目的是为了便于在大气媒质中传播，并且在某些情况下还能提高抗干扰能力。各种类型的调幅（AM）都是线性调制，而调频和调相（一般统称为调角）为非线性调制。

下面通过两种途径来探讨模拟通信系统中信号的波形估计问题：① 利用最大后验概率法，得到一个积分方程；② 利用状态变量法，得到卡尔曼滤波器。前者解积分方程得到消息的估计量。只要精心利用该结果，可以得到一些实际的接收机结构。后者假定消息是白噪声激励线性系统产生的输出。视调制的方式不同，观测模塑可能是线性的或非线性的。适当地扩充消息模型，可以把一些效应如信道的衰落效应等考虑进来。这时模型通常是非线性的。无论哪种情况，可用非线性卡尔曼滤波算法，求得适当的接收机结构。

本节将针对一些具体情况来介绍第一种方法，利用最大后验概率准则求调幅和调角两种情况下接收机的结构。

下面研究模拟通信系统中信号x（t）的估计问题。假定信号x（t）是随机过程的一个样本函数，将它以线性或非线性方式去调制载波。在加性白高斯噪声v（t）中观测已调的信号y [ x（t），t ]，因此，观测波形为

本式所示的观测模型，依y [ x（t），t ]的形式不同，可以用来描述几种常见的模拟调制方式。例如：

其中，上式表示双边带、抑制载波调幅（DSB-SC-AM）。如果已调信号是

那么该信号就是双边带调幅（DSB-AM）。其中，α 是标量，称作调制指数。这种调制方式下载波分量也照样发送。在这两种载波调幅情况下，已调信号是线性的。

在调角情况下，载波的相位或频率随信号x（t）而变化。在调相（PM）情况下，已调信号是

其中，β 也是调制指数。信号x（t）在y（x（t），t）中是以非线性的方式出现的。

更一般地，信号x（t）可先通过一个线性（通常是时不变的）滤波器（预加重网络），将信号的频谱改变成合乎某种要求的形式。已调信号是

其中，h（t，τ）是滤波器的冲激响应。图7-1 画出了一般模拟调制系统的基本组成部分，设θ（t）表示滤波器的输出。(www.daowen.com)

图7-1　模拟调制系统

如果预加重网络是一个积分器，则可转化为

这时得到的是调频（FM）。使用预加重滤波调制方式的另外一个例子是残留边带调幅（VSB-AM），这种调制方式已经广泛用来传输视频信号。在残留边带调幅方式中，信号x（t）同时通过两个线性时不变滤波器，这两个滤波器的冲激响应分别为hc（t，τ）和hx（t，τ）。两个滤波器的输出；xc（t）和xs（t）分别对两个载波进行调幅，两个载波频率相同，但相位彼此差90°，如图7-2 所示。其中，已调信号是

图7-2　残留边带调制系统

特殊情况下，当xc（t）= x（t）、xs（t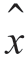）= （t）时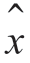，（t）表示x（t）的希尔们特变换，信号经希尔伯特变换后，在频域各频率分量的幅度保持不变，但相位将出现90°相移，则该调制方式对应于单边带调幅（SSB-AM）。此时，假定信号是高斯过程，利用波形估计的最大后验方程可以推导出观测模型的估计方程，即

图7-3 画出了估计器的方框图。因为估计量是根据整个区间[t0， t1]上的观测量得出来的，所以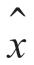，（t）实际上是基于整个区间[t0， t1]内观测值记录的平滑估计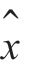（u|t1），而且该估计器是物理上不可实现的，我们在推导调角系统最大后验接收机时再详细地讨论。

图7-3　模拟调制用的最大后验估计器

现在研究具有预加重滤波的调制系统。设外θ（t）表示滤波器的输出，如图7-1 所示。利用类似的方法可给出最大后验方程，即

其中，h（σ，u）表示预加重滤波器的冲激响应，即

下面就调幅和调频这两种具体情况讨论接收机的结构。