本节通过一个例子来说明序列检测相对于固定观测次数检测的优越性，二者比较的条件是每次采样的信噪比相同，表征检测性能的虚警概率和检测概率相同。比较的结果必然是序列检测的平均观测次数少于固定观测次数检测的观测次数。

设在高斯噪声干扰下，恒定电压信号的序列检测问题，其两种假设为

式中，si=a 表示电压信号；高斯噪声样本ni 的均值为0，方差为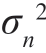，并且各样本相互统计独立。

在假设H1 和假设H0 下，所需的平均观测次数为

在等取样间隔Δt 条件下，有信号和无信号时，序列检测的平均检测时间分别E[m|H_1]Δt 为和E[m|H_0]Δt。

在相同条件下，对于固定观测次数检测，设观测次数为k，k 个独立的观测样本组成的向量xk=[x1，x2，…，xk]T。当有信号时，似然函数

式中，yk 为检测统计量。因为xi 是独立同分布的高斯随机变量，故yk 也是高斯随机变量。

在假设H1 和假设H0 下，yk 的数学期望为

在假设H1 和假设H0 下，为了对序列检测与固定观测次数检测进行比较，将序列检测的平均观测取样数与固定观测次数检测的观测样本数之比定义为取样数缩短因子。并绘出假设H1 和假设H0 下取样数缩短因子与发现概率Pd 的函数关系曲线，如图6-2 所示。由图6-2 可以看出：

（1）在给定条件下，无论发现概率为何值，序列检测的平均取样数都比固定观测次数检测的取样数少，都不超过固定取样数的70%。(www.daowen.com)

（2）无信号时序列检测相对于固定观测次数检测的取样数缩短因子比有信号时的取样数缩短因子小，即益处更大。

图6-2　取样数缩短因子与发现概率的关系曲线

（3）取样数缩短因子基本上是发现概率的递增函数。发现概率越小，取样数缩短因子也越小，因而序列检测的优越性就越显著。

根据上述结论可以看出，序列检测最好应用于如下场合：①α ＜＜β；②无信号时的先验概率P（H0）远大于有信号时的先验概率P（H1）。雷达就属于后一种情况，因此序列检测适合于雷达，可使总平均取样数达到最小，从而节省了雷达搜索目标的时间，提高了搜索的效率。

总之，固定观测次数（观测样本数）检测或固定观测时间检测是在观测次数（观测样本数）或观测时间事先确定的情况下，使检测性能达到最佳的检测方法，其存在观测次数（观测样本数）或观测时间不能自动适应检测性能或接收信号信噪比的不足。于是，序列检测被提出。

固定观测次数检测或固定观测时间检测是在给定观测次数或观测时间的情况下，使检测性能最佳。序列检测是在给定检测性能的情况下，使观测次数最少或观测时间最短。固定观测次数检测或固定观测时间检测采用先观测后判决的方式，也就是完成事先规定观测次数或观测时间后，根据所有观测样本做出判决。序列检测采用边观测边判决的方式，也就是事先不规定观测次数或观测时间的情况下，按自然顺序观测接收信号得到观测样本，随时根据观测样本进行处理和做出判决。

本章主要讨论了二元序列检测的基本原理。二元序列检测采用统一的似然比检测方法，各种判决准则的不同体现在检测门限中。但是，二元序列检测的检测门限需要两个。在二元序列检测中，采用修正的奈曼-皮尔逊准则的序列检测是应用较广的一种，它是在给定虚警概率和漏报概率的条件下，确定似然比双门限值，通过逐步观测并进行似然比检测，以达到检测性能指标的准则。

序列检测的突出优点是在给定的检测性能要求下，所用的平均观测次数最少或平均检测时间最短。与固定观测次数检测相比，一般情况下序列检测可节省1/2以上样本数。它的缺点是，在检测的每一步都要重新调整检测统计量，并在做出判决之前还必须存储用过的样本。