对于一般二元随机相位信号的检测，设发送设备发送的二元信号为

式中，a（t）和b（t）为振幅；ω0 和ω1 为频率，且频差ω1-ω0 很小；θ0 和θ1为相位，均是随机变量，其先验概率密度p（θ0）和p（θ1）在区间（0，2π）上为均匀分布。

假设接收设备接收的信号为窄带信号，对应的两种假设为

式中，n（t）是窄带高斯色噪声，其均值为0，相关函数为Rn（τ）。本式所示假设模型的典型应用实例是一般二元通信系统信号的检测。

在假设H1 下，有用信号可以表示为

式中，A（t）=a（t）exp[j（ω1-ωc ）t]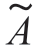，（t）=A（t）exp[jθ1]是信号s1（t，θ1）的复包络；ωc 是窄带信号的中心频率，也就是载波频率。假定频差ω1-ωc 很小，因而A（t）是时间的慢变化函数。在假设H0 下，有用信号可以表示为

式中，B（t）=b（t）exp[j（ω0-ωc ）t]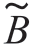，（t）=B（t）exp[jθ0] 是信号s0（t，θ0）的复包络；假定ω0-ωc 频差很小，故B（t）是时间的慢变化函数。

基于复包络的一般二元随机相位信号检测的假设为

式中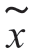，（t）是接收信号x（t）的复包络；（t）是窄带高斯色噪声n（t）的复包络。

（一）检测算法

采用简单二元随机相位信号似然函数的分析方法，可以得到两种假设下的似然函数。在假设H1 下，复包络（t）的平均似然函数为

式中，xk 为复包络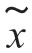（t）的卡亨南-洛维展开系数；Ak 为A（t）的卡亨南-洛维展开系数；统计量D1 为

式中，滤波器冲激响应的复包络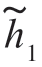（t）是以下积分方程的解

在假设H0 下，复包络（t）的平均似然函数为

式中，Bk 为B（t）的卡亨南-洛维展开系数；统计量D0 为

式中，滤波器冲激响应的复包络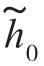（t）是以下积分方程的解(www.daowen.com)

似然比为

相应的对数似然比为

式中

设检测门限为Λ0，高斯色噪声中一般二元随机相位信号检测的判决式为

（二）检测系统结构

由高斯色噪声中一般二元随机相位信号检测的判决式可知，检测系统需要提取统计量D0 和D1，而提取D0 和D1 需要将接收信号x（t）送入复冲激响应为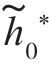（T-t）和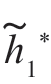（T-t）的带通滤波器来实现。D0 和D1 的表达式中绝对值的含义是指对带通滤波器输出的包络进行抽样。

滤波器冲激响应的复包络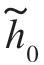（t）和（t）是式（5.4.61）和式（5.4.58）所示积分方程的解。滤波器的冲激响应为

根据高斯色噪声中一般二元随机相位信号检测的判决式，可以得到相应检测系统的结构，如图5-4 所示。

图5-4　高斯噪声中一般二元随机相位信号的最佳检测系统

总之，高斯色噪声中信号的检测是将信道噪声具体为高斯色噪声，也就是将前文所讨论的信号检测的基本理论应用于高斯色噪声中的信号检测。

由于高斯色噪声的自相关函数不再是函数，故高斯色噪声在任意两个不同时刻的取值不再是不相关的。因此，利用时域采取样定理的方法来研究高斯色噪声中信号的检测已经不适用了。

高斯色噪声中信号检测的基本方法通常有两种：一种是采用匹配滤波器中的白化处理方法，先将含有高斯色噪声的接收信号转换为含有高斯白噪声的信号，然后再按白噪声中信号检测的方法进行处理。另一种是卡亨南-洛维展开方法。本章主要讨论了采用卡亨南-洛维展开的高斯色噪声中信号检测的方法。

采用卡亨南-洛维展开的高斯色噪声中信号检测的方法就是将含有高斯色噪声的信号表示成正交展开的形式，将正交展开的系数作为样本，从而使样本是相互统计独立的。通过求取卡亨南-洛维展开系数的概率密度，并将它们相乘，得到所有卡亨南-洛维展开系数的联合概率密度，再由卡亨南-洛维展开系数的联合概率密度得到不同假设下的似然函数，从而就可以依据似然比检验方法进行信号检测。

本章主要讨论了高斯色噪声中确知信号和随机相位信号的检测。有兴趣的读者可以在高斯色噪声中随机相位信号检测的基础上，继续深入讨论高斯色噪声中随机振幅和相位信号的检测、随机频率和相位信号的检测、随机相位和到达时间信号的检测、随机振幅、频率和相位信号的检测、随机频率和到达时间信号的检测。

本章所讨论的信号检测是以信道噪声为平稳的高斯色噪声为前提条件的，高斯色噪声的平稳性是通过其相关函数Rn（τ）来体现的，希望读者注意这一点。