对于简单二元随机相位信号的检测，设发送设备发送的二元信号为

式中：A（t）为振幅；ω 为频率；θ 为相位，是随机变量，其先验概率密度p（θ）在区间（0，2π）上为均匀分布，即

相位均匀分布意味着完全缺乏相位信息，是一种最不利的分布。

接收设备检测信号对应的两种假设为

式中，n（t）是窄带高斯色噪声，其均值为0，相关函数为Rn（τ）。式（5.4.18）所示假设模型的典型应用实例是具有随机初相的窄带雷达单个回波信号的检测。

信号的信息完全由其复包络携带，载波仅起到载体的作用，故只需用复包络就可以进行信号检测问题的研究。

基于复包络的简单二元随机相位信号检测的假设为

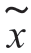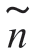式中，（t）是接收信号x（t）的复包络；是随机相位信号s1（t，θ）的复包络；（t）是窄带高斯色噪声n（t）的复包络。

（一）似然函数

在假设H1 下，接收信号x（ t）的复包络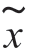（t）的卡亨南-洛维展开为

式中，fk（t）满足以下积分方程

式中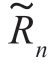，（τ）为噪声自相关函数Rn（t）的复包络。展开系数为

因此，可以证明

这表明复包络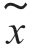（t）的展开系数xk 是不相关的，由于它们又是高斯的，因此它们是统计独立的。

复包络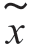（t）的卡亨南-洛维展开的前m 个展开系数的联合概率密度就等于各个展开系数概率密度的乘积。展开系数包含实部αk 和虚部βk 两个变量，故展开系数是二元高斯随机变量。要得到展开系数的概率密度，就需要求出实部αk 和虚部βk 的均值、方差及相关系数。

可以证明，并由此得到

当k = i 时，可得(www.daowen.com)

进而通过联立求解，得到

可见，展开系数xk 实部和虚部是统计独立的。xk 的实部和虚部的方差都等于特征值λk。于是，只需求出实部和虚部的均值，就可以写出xk 的概率密度。

在假设H1 下，复包络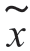（t）的展开系数xk 的均值为

式中，Ak 为振幅A（t）的展开系数。

在假设H0 下，相当于信号振幅A（t）=0 的情况，统计量D=0，I0（D）=1，滤波器冲激响应的复包络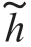（t）=0，故复包络（t）的似然函数为

（二）检测算法

高斯色噪声中简单二元随机相位信号的检测仍采用似然比检验方法。似然比为

设检测门限为Λ0，高斯色噪声中简单二元随机相位信号检测的判决式为

其等效检测判决式为

由于I0（D）是统计量D 的单调增函数，故检测判决式可以写成

式中，β 为对应检测统计量D 的检测门限。

（三）检测系统结构

由高斯色噪声中简单二元随机相位信号检测的判决式可知，检测系统需要提取检测统计量D，而提取D 需要将接收信号x（t）送入复冲激响应为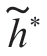（T-t）的带通滤波器来实现。D 的表达式中绝对值的含义是指对带通滤波器输出的包络进行抽样。滤波器冲激响应的复包络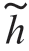（t）是相关积分方程的解。滤波器的冲激响应为

可以得到相应检测系统的结构，如图5-3 所示。

图5-3　高斯色噪声中简单二元随机相位信号的最佳检测系统