在随机参量信号为正弦信号的检测中，最常见的随机参量是相位。如许多通信系统中，接收信号的相位不仅取决于发射信号的初相，而且还取决于路径上的延时。在假定随机相位的先验概率密度已知的情况下，下面分两种情况来讨论二元随机相位信号的检测：简单二元随机相位信号的检测和一般二元随机相位信号的检测。

简单二元信号的检测是指一种假设下不存在有用信号，而另一种假设下存在有用信号。它适用于雷达、声呐和通断型二元通信系统。一般二元信号的检测是指两种假设下均存在有用信号。它适用于一般二元通信系统。

（一）简单二元随机相位信号的检测

对于简单二元随机相位信号的检测，设发送设备发送的二元信号为

式中，A 为振幅；ω 为频率；θ 为相位，是随机变量，其先验概率密度p（θ）在区间（0，2π）上为均匀分布，即

相位均匀分布意味着完全缺乏相位信息，是一种最不利的分布。

接收设备检测信号对应的两种假设为

式中，n（t）是均值为0，功率谱密度为N0/2 的高斯白噪声。本式所示假设模型应用的典型实例是具有随机初相的窄带雷达单个回波信号的检测。

下面讨论高斯白噪声中简单二元随机相位信号的检测算法、检测系统的结构及检测性能。

1.检测算法

二元信号的检测都可以归结为似然比检测，不同的判决准则只影响门限值的大小，因此下面按照似然比检测来讨论，无须指定具体的准则。

一般情况下，代价与θ 无关，因而其平均似然比判决规则为

式中，Λ0 为判决门限，它取决于所采用的判决准则。

要计算似然比，首先需计算似然函数。在假设H0 下，接收信号x（t）=n（t），其似然函数为

式中，F 为与信号无关的常数。

在假设H1 下，接收信号x（t）=A sin（ωt+θ）+n（t），其似然函数为

因为p（x|θ，Hi）中含有随机参量θ，需要将p（x|θ，Hi）对θ 求统计平均，得到平均似然函数。

2.检测系统结构

根据高斯白噪声中简单二元随机相位信号的检测算法，可以得到相应检测系统的结构，如图4-14 所示，它是由正交的两个支路构成的，故称为正交双路检测系统，通常称为正交接收机。

图4-14　正交双路检测系统

图4-14 所示的正交双路检测系统结构还可以进一步简化。为此，设计一个与sinωt 相匹配的滤波器，其冲激响应为

当接收信号x（t）输入到该滤波器时，其输出为

当t = T 时，y（t）的包络值为

正好与所示的检测统计量M 一致。这说明，使接收信号x（t）通过一个与信号sinωt 匹配的滤波器，然后再通过一个包络检波器，在t = T 时刻的输出与正交双路检测系统的输出相同，都是M。匹配滤波器和包络检波器的组合常称为非相干匹配滤波器，如图4-15 所示。可以进一步证明，对信号任何一个相位匹配的滤波器，都可以组成非相干匹配滤波器。

图4-15　非相干匹配滤波器(www.daowen.com)

3.检测性能分析

高斯白噪声中简单二元随机相位信号检测算法的关键是计算检测统计量M 的值，然后再与门限值β 进行比较。由于检测算法的检测统计量为M，若要分析高斯白噪声中简单二元随机相位信号检测算法或检测系统的检测性能，首先需要求出M 的条件概率密度。

由于，若要求M 的条件概率密度，一般需要先求出M1 和MQ的联合概率密度，然后通过M 与M1 和MQ 的关系，用雅可比变换来求出M 的条件概率密度。由于x（t）服从高斯分布，而M1 和MQ 都是x（t）经过线性变换得到的，所以M1 和MQ 也是高斯随机变量，只要求出它们的条件数学期望及方差，便可确定它们的条件概率密度函数。由于随机变量M1 和MQ 是由相位相差90°的通道获得的，可以证明它们不相关，因而是统计独立的。

（二）一般二元随机相位信号的检测

对于一般二元随机相位信号的检测，设发送设备发送的二元信号为

式中，A 为振幅；ω0 和ω1 为频率，且一者不同，相隔较远；θ0 和θ1 为相位，均是随机变量，其先验概率密度p（θ0）和p（θ1）在区间（0，2π）上为均匀分布。设ω0 T=k0 π，ω1 T=k1 π，k0 和k1 均为正整数。信号s0（t，θ0 ）的能量为E0=A2 T/2，信号s1（t，θ1 ）的能量为E1=A2 T/2，且E0=E1=E。

接收设备检测信号对应的两种假设为

式中，n（t）是均值为0，功率谱密度为N0/2 的高斯白噪声。上式所示假设模型应用的典型实例是一般二元通信系统信号的检测。

1.检测算法

在假设H0 下，接收信号x（t）=A sin（ω0 t+θ0） +n（t），其似然函数为

因为p（x|θ0，H0）中含有随机参量θ0，需要将p（x|θ0，H0）对θ0 求统计平均，得到平均似然函数，即

于是一般二元随机相位信号检测的检测判决式为

式中，Λ0 为判决门限，它取决于所采用的判决准则。

在二元通信系统中，通常采用最小平均错误概率准则，即c00=c11=0，c01=c10=1。如果假设的先验概率P（H0）=P（H1），判决门限Λ0=0，则一般二元随机相位信号检测的检测判决式简化为

由于修正的零阶第一类贝塞尔函I0 （x）是其变量的单调增函数，故以I0 （2AM/N0）进行判决完全等效于以统计量M 进行判决，于是，检测判决式可以写为

2.检测系统结构

根据高斯白噪声中一般二元随机相位信号的检测算法，可以得到相应检测系统的结构，如图4-16 所示。当然，图4-16 中的开方运算可以省去，检测统计量M0 和M1 分别可由匹配滤波器和包络检波器组成的非相干匹配滤波器获得。

图4-16　一般二元随机相位信号检测系统

3.检测性能分析

对于高斯白噪声中一般二元随机相位信号的检测，为了能得到检测性能的解析结果，假定两个信号的频率ω0 和ω1 满足ω1=kω0，k 为大于1 的整数，这意味着信号s0 （t，θ0 ）与s1 （t，θ1 ）是两个正交信号。这样，在假设H1 为真时，图4-16 所示检测系统的上半支路输出随机相位信号s1 （t，θ1 ）加高斯白噪声的包络M1，而下半支路输出高斯白噪声的包络M0。因此，M0 和M1 分别相当于简单二元随机相位信号检测时，在假设H1 和假设H0 为真时的检测统计量。于是，可以利用简单二元随机相位信号检测系统性能分析的结果来分析一般二元随机相位信号检测系统性能。

由于两种信号能量相等，即E0=E1= E=A2 T/2，且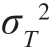=N0 T/4，因此，在假设H1 为真时，检测统计量M1 的概率密度为

检测统计量M0 的概率密度为

在假设H1 为真时，如果检测统计量M1 ≥ M0，则判决D1 是正确的，否则将出现错误判决D0。所以，错误判决概率为

最小平均错误概率为