为了解决多元确知信号的一般检测方法分析错误概率困难的问题，可以采用正交检测方法。

（一）检测算法

设确知信号sk（t）的能量为Ek，信号si（t）与sk（t）的相关系数为

对于白噪声n（t），取任意正交函数集{fj（t） }将平稳随机过程x（t）=s（t）+n（t）进行展开，其展开系数xj（j = 1，2，…）之间都是互不相关的。这就是白噪声情况下正交函数集的任意性。根据这一性质，能够利用格拉姆-施密特正交化方法来构造一个与各假设中的信号sk（t）相联系的正交函数集{fj（t） }，使各假设Hk 下，接收信号x（t）的正交级数展开系数xkj 互不相关，从而形成各假设下的似然函数，建立似然比检测。

根据格拉姆-施密特正交化方法，令

为正交函数集{fj（t） }的第1 个坐标函数，它是对g1（t） =s1（t）归一化得到的。令

为正交函数集{fj（t） }的第2 个坐标函数，它是对与f1（t）正交的函数

归一化得到的。令

它是对与f1（t）和f2（t）正交的函数g3（t）归一化得到的，其中，系数c1 和c2是构造g3（t）时产生的，而系数c3 是对g3（t）归一化获得正交函数集{fj（t） }的第3 个坐标函数f3（t）时形成的。这样进行下去，获得正交函数集{fj（t） }的第4 个坐标函数f4（t），第5 个坐标函数f5（t），直到第M 个信号sM（t）被用来构造出第M个坐标函数fM（t）为止。对正交函数集{fj（t） }中，j ≥ M+1 的坐标函数{fj（t） }，具体函数形式不必设计。

在用信号s1（t），s2（t），…，sM（t）构造正交函数集{fj（t） }的坐标函数f1（t），f2（t），…的过程中，如果这M 个信号s1（t），s2（t），…，sM（t）是线性不相关的，那么，能够构造出M 个正交函数集{fj（t） }的坐标函数f1（t），f2（t），…，fM（t）。如果这M 个信号s1（t），s2（t），…，sM（t）中，只有N 个信号是线性不相关的，而其余的M-N 个信号的每一个可由其余信号的线性组合来表示，那么，能够构造出N个正交函数集{fj（t） }的坐标函数f1（t），f2（t），…，fN（t）。对于这两种情况，根据M 个信号s1（t），s2（t），…，sM（t）构造的正交函数集{fj（t） }的坐标函数，统一地记为f1（t），f2（t），…，fN（t），N ≤ M，j ≥ N +1 的坐标函数{fj（t） }不需要具体设计。

利用构造的N 个正交坐标函数fj（t）（j = 1，2，…，N），对任意假设下的接收信号x（t）进行正交级数展开，级数展开的前N 个展开系数为

由于噪声n（t）是高斯白噪声，因而接收信号x（t）是高斯平稳随机过程。正交函数集{fj（t） }的坐标函数fj（t）是由信号s1（t），s2（t），…，sM（t）构造出来的，因而坐标函数fj（t）是确知函数。因此，接收信号x（t）的前N 个展开系数xj 是相互统计独立的高斯随机变量。

展开系数xj 的均值取决于假设Hk，即在假设Hk 下展开系数xj 的均值为

在假设Hk 下展开系数xj 的方差为

可见，展开系数的方差与哪个假设Hk 为真无关，都是N0/2。

由于展开系数xj 之间是互不相关的，所以xj 与xi 之间的协方差Cji=0（j ≠i），Cjj=Var[xj |Hk ]。

由N 个展开系数构成N 维随机向量，即

在假设Hk 下，x 的均值向量为

在每个假设下，x 的协方差矩阵为

于是，在假设Hk 下，高斯随机向量x 的N 维联合概率密度函数为

对于最小平均错误概率准则，代价因子cki=1-δki（k，i=1，2，…，M），此时，使平均错误概率最小的准则等价为最大后验概率准则。所以，采用最小平均错误概率准则的M 元信号检测，需要计算各假设下的后验概率P（Hi|x）（i=1，2，…，M），选择P（Hi|x）中最大的P（Hk|x）=max{ P（Hi|x），i=1，2，…，M}对应的假设Hk成立。即表示为：

若(www.daowen.com)

则判决假设Hk 成立。这个问题也可以等价地表示为：

若

则判决假设Hk 成立。

因为P（x|Hi）是N 维联合高斯概率密度函数，上式可以进一步化简为

则判决假设Hk 成立。

如果进一步假定：各假设Hi 为真的先验概率P（Hi）相等，即P（Hi）=1/M，i=1，2，…，M，则上式化简为

则判决假设Hk 成立。可以进一步化简为

则判决假设Hk 成立。如果令

检测判决算法为：

若

则判决假设Hk 成立。

因为检测统计量Gi 也可以表示为连续信号的形式，即

故检测判决算法为：若

则判决假设Hk 成立。对应的最佳检测系统如图4-13 所示。

图4-13　元相关确知信号的最佳检测系统

（二）检测性能分析

多元相关确知信号检测系统的检测性能仍然是平均错误概率，即

其基本方法仍然是先求出各假设Hi 下各检测统计量Gk 的概率密度函数p（Gk|Hi），然后根据判决式对p（Gk |Hi）在相应区间积分，得到各判决概率P（Dk |Hi），最后计算平均错误概率。

如果各假设出现的先验概率P（Hi）相等，则平均错误概率为

如果各假设出现的先验概率P（Hi）相等，且各假设下信号的能量相等，则各假设的错误判决概率相等，平均错误概率为

式中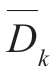，代表错误判决。