雷达回波信号的检测是二元信号的检测问题。相干雷达对固定目标回波信号的检测就是二元确知信号的检测问题，其假设空间为Θ={H0，H1}，两种假设表示为

式中，n（ t）是均值为0、方差为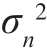、功率谱密度为N0/2 的高斯白噪声；T 为接收设备观测接收信号x（ t）的时间。在此，s0（ t）=0，s1（ t）是确知的目标回波信号。假设H0 代表目标不存在，假设H1 代表目标存在。针对本式所示假设空间的信号检测也称为简单二元信号的检测。

相干雷达对固定目标回波信号检测的检测统计量为

则回波信号检测的判决式为

图4-9　相干雷达的最佳检测系统

对于雷达情况，通常无法事先确定先验概率和代价因子，因而采用奈曼-皮尔逊准则，即在给定虚警概率Pf 的条件下，使检测概率Pd 达到最大。此时最佳检测系统的框图如图4-9 所示，判决门限β 则由给定的Pf 确定

虚警概率

检测概率为

对于相干雷达情况，有rK =0，E0=0，EK =E1 /2。在假设H0 条件下，x（t）=n（t），此时的检测统计量为

它也是高斯随机变量，均值E[G|H0]=0，方差Var[G|H0]=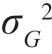=N0 E1/2，因此，假设H0 下检测统计量G 的条件概率密度函数为(www.daowen.com)

在假设H1 条件下，x（t） = s1（t） + n（t），此时的检测统计量为

它也是高斯随机变量，均值为E[G|H1]=E1，方差为Var[G|H1]=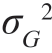=N0 E1/2，因此，假设H1 下检测统计量G 的条件概率密度函数为

由假设H0 下检测统计量G 的条件概率密度函数得到虚警概率为

式中，

由假设H1 下检测统计量G 的条件概率密度函数得到检测概率为

式中，

对于给定的虚警概率Pf，可算出，再将此值及选定的信噪比代入上式，即可算出检测概率Pd，从而可得到系统的检测性能曲线。可看出，当Pf 给定之后，Pd 只与信号能量E1 及噪声谱密度N0 之比有关，而与信号s1（ t）的波形无关。这便是检测理论中有名的能量原理。根据绘成的以Pf 为参变量的曲线，称为相干雷达系统的检测特性曲线，常称为接收机的工作特性曲线，如图4-10 所示。根据给定的Pf 和输入信噪比，由图4-10可以方便地求出Pd，因此检测特性曲线可用于相干雷达系统的设计。根据Pd、Pf与输入信噪比的关系，也可以用输入信噪比作为参变量，画出Pd 与Pf 的曲线作为系统的检测性能曲线，如图4-11 所示。

图4-10　相干雷达的检测特性曲线

图4-11　检测概率与虚警概率的关系曲线