对于理想高斯白噪声，只有在相同时刻才相关，而在任意两个不同时刻上采样值都是不相关的，满足不相关的要求。但是，理想高斯白噪声的带宽无穷大，不满足采样定理的要求，不能用离散的采样值来代替连续时间随机信号。如果对理想高斯白噪声的采样间隔Δt 趋于0，而不等于0 时，仍可以保证任何两个采样值不相关。为了满足采样定理和不相关要求，对理想高斯白噪声的采样间隔Δt 应趋于0，成为连续采样情况。因此，理想高斯白噪声中二元确知信号的检测需要对接收信号连续采样，而接收信号的连续采样就是其连续函数形式或连续波形。理想高斯白噪声中二元确知信号检测的判决式也就用连续函数来表示。

为了方便，通过将带限白噪声转变为理想白噪声的方法，研究理想高斯白噪声中二元确知信号的检测。在观测时间T 不变的情况下，使采样间隔Δt 趋于0，相应的采样数N 趋于无穷大，带限白噪声的带宽Ω=π/Δt 趋于无穷大，这样，带限白噪声变为理想白噪声，离散采样变为连续采样。

为了得到连续接收信号的似然函数，将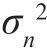=N0/2Δt 代入到各种假设下观测向量x 的似然函数中，有

在NΔt=T 保持为常数的条件下，使采样间隔Δt 趋于0，采样数N 趋于无穷大的极限情况下，便得到连续接收信号x（t）的似然函数为

式中，F 为一常数。

连续接收信号x（t）的似然比为

连续接收信号x（t）的似然比检测判决式为(www.daowen.com)

或者

令

式中，β 为判决门限；E1 和E0 分别表示确知信号s1（t）和s0（t）的能量，即

故连续接收信号x（t）的似然比检测判决式又可简写为

根据本式就可以得到高斯白噪声中二元确知信号的最佳检测系统，其原理框图如图4-8 所示。图4-8 就是通常所说的相关接收机，它通过计算接收信号x（t）与确知信号s1（t）和s0（t）的互相关，相减后再与判决门限β 比较，最后做出判决。

图4-8　二元确知信号的最佳检测系统