对于带限高斯白噪声，自相关函数Rn（t）在τ = kπ /Ω（k =±1，±2，…）处为0，说明接收信号按τ = kπ /Ω 的时间间隔进行采样，得到的各样本是不相关的，又由于是高斯分布的，所以它们又是统计独立的。

对于接收信号x（t）=s（t）+ n（t），通常有用信号s（t）的频带宽度小于噪声n（t）的频带宽度，故接收信号x（t）的频带宽度为噪声n（t）的频带宽度Ω。以采样间隔Ts ≤ π /Ω 对接收信号x（t）进行采样，得到随机序列为x （kTs ）。

为了保证对接收信号采样后的信息不丢失和采样序列x（kTs）的不相关，采样间隔Δt 需同时满足Δt ≤ π /Ω 和Δt = kπ /Ω，故采样间隔取为Δt = π /Ω。也就是说，对接收信号的采样既要满足采样定理要求，也要满足不相关要求。满足采样定理可以保证对接收信号采样后的信息不丢失。满足不相关要求可以使所有采样值的联合概率密度等于每次采样值概率密度的乘积。在带限高斯白噪声情况下，用满足采样定理和不相关要求的采样值来代替连续时间随机信号。

设采样间隔Δt =π /Ω，x（t）、si（t）和n（t）在t = kΔt 时刻的采样值记为xk、sik 和nk。在观测时间（0，T）内，采样数目为

对噪声n（t）、有用信号s0（t）、s1（t）和接收信号x（t）的N 个采样值分别定义为噪声向量n、信号向量s0、信号向量s1 和观测向量x 如下：

由于带限高斯白噪声n（t）的均值为0，方差为

故噪声n（ t）的采样值nk 是均值为0、方差为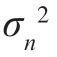的高斯随机变量。由于xk =sik+nk，且sik 是确定值，故xk 是高斯随机变量，其条件均值为

其条件方差为

故xk 的条件概率密度函数为

由于接收信号x（t）是高斯随机信号，其N 个采样值是不相关的，也就是统计独立的。因此，观测向量x 的似然函数等于每次采样值的似然函数乘积。在假设H0 下，观测向量x 的似然函数为(www.daowen.com)

在假设H1 下，观测向量x 的似然函数为

观测向量x 的似然比为

似然比检测方法的一般检测判决式为

式中，Λ0 为似然比门限，取决于所选用的最佳准则。

根据似然比检测方法的一般检测判决式，得到带限高斯白噪声中二元确知信号检测的检测判决式为

或者

如果将式（4.2.14）中的判别号改为等号，就可以得到对接收信号进行N 次观测时的判决界限，即

在一般情况下，维空间内的判决界限可能是一个曲面，本式仅是在高斯信道内检测确知信号的一个特例。