奈曼-皮尔逊准则就是指在虚警概率PF=α 的约束条件下，使检测概率PD 最大的准则。

奈曼-皮尔逊准则限定PF=α 根据这个约束，设计使PD 最大（或PM=1-PD 最小）的检验。应用拉格朗日（Largrange）乘子μ（μ ≥ 0），构造一个目标函数

显然，若PF=α，则J 达到最小，PM 就达到最小。变换积分域，为

因为μ≥0；所以本式中第一项为正数，要使J 达到最小，只有把式中方括号内的项为负的x 点划归R0 域，判H0 成立；否则划归R1 域，判H1 成立，即

写成似然比检验的形式为

为了满足PF=α 的约束，选择μ 使

于是对于给定的α，μ 可以由上式求出。

因为0 ≤ α ≤ 1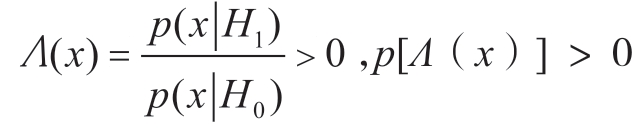，，所以解出的μ 必满足μ ≥ 0。(www.daowen.com)

现在说明似然比检测门限μ 的作用。类似式有

显然，μ 增加，PF 减小，PM 增加；相反，μ 减小，PF 增加，PM 减小。这就是说，改变μ 就能调整判决域R0 和R1。

奈曼-皮尔逊准则可看成是贝叶斯准则在P（H1）（c01-c11）=1，P（H0）（c10-c00）=μ 时的特例，μ 为似然比检测门限，仍可用η 的函数表示。

由上可知奈曼-皮尔逊准则的最佳检验是由三个步骤完成的：

① 对观测量x 进行加工，求出似然比检验式并进行化简，得检验统计量l（x）的判决规则表示式、检测门限η；

② 根据检验统计量l（x）与检测门限η 的判决规则表示式，由PF=α 的约束求出检测门限η′（是似然比检验门限η 的函数）；

③ 完成判决，得出结论。