优化准则需要知道各种判决的代价和假设的先验概率P（Hi）（i = 0，1）。但有时只知道判决的代价Cij（i，j = 0，1），而不知道假设的先验概率P（Hi）（i = 0，1）。此时，通常的做法就是寻找某一个先验概率作为代表，用它计算门限，用该门限组成似然比处理器，使得不论实际上假设的先验概率如何，其风险都不超过用“先验概率代表”计算的风险。寻找平均风险中最大者对应的先验概率作为这个“代表”，即为寻找贝叶斯检验中的最不利先验概率，因此称这个准则为极小化极大准则。

极小化极大准则的关键是寻求那个最不利的先验概率，有了它就可以计算检验门限。首先，我们知道判决风险为

令P1= P（H1）， P（H0）=1- P（H1）， 又PF= P（H1|H0），P（H0 |H0）=1-PF，PM= P（H0|H1）， P（H1 |H1）=1-PM，将这些关系代入上式，经整理后可得

对于给定的P1，如果按照贝叶斯准则确定判决门限，即

那么，计算所得的风险是对应于先验概率P1 的最小风险，即贝叶斯风险可表示为

很显然，不同的先验概率P1、判决门限不同，对应的最小风险也不同。可以证明，风险是严格凸函数，由此可以画出一条最小风险随先验概率P1 变化的曲线，如图3-7 中的曲线4 所示。

图3-7　最小风险与先验概率P1 的关系曲线

由图3-7 可以看出，存在一个先验概率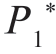，对应的最小风险达到最大，这个先验概率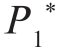称为最不利的先验概率。(www.daowen.com)

现在考虑不知道先验概率P1 的情况，为了能采用贝叶斯准则，只能猜测一个先验概率P1·，用这个先验概率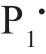确定贝叶斯判决门限，此时PF 和PM 都是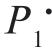的函数，记为PF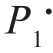（）和PM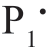（）。此时的风险为

C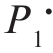（，P）与P1 的关系是一条直线，如图3-7 中的曲线B 所示。很显然，C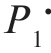（，）= C_min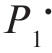（），即当猜测的先验概率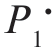恰好等于实际的先验概率P1 时，风险达到最小，即为贝叶斯风险，所以直线C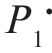（，P）与Cmin（P1）在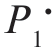= P 处相切。

由图3-7 可以看出，当实际的P1 与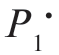相差不大时，风险与最小风险相差不大；当实际的P1 与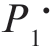相差较大时，风险会变得很大，如图3-7 中P2 只对应的风险，我们不希望出现这样的情况；如果选择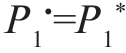，这时风险是平行于横轴的，这时的风险不随P1 变化，是个恒定值。极小化极大准则就是根据最不利的先验概率确定门限的一种贝叶斯判决方法，这时的风险是一个恒定值，不随先验概率变化。要使风险为常数，可令直线斜率为零，从而解出最不利的先验概率。

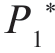上式称为极小化极大方程，通过令最小风险对P1 的导数为零也可以求得最不利先验概率，即

当c11=c00=0，c01=c10=1 时，本式可简化为

此时的平均代价等于总错误概率。