（一）重要采样原理

设y 为随机变量，其概率密度函数为p（y），分布函数为P（y）。计算y 超过门限Y 的概率（若y 表示噪声，则该概率即为虚警概率）

在实际问题中，上面的积分往往不能用解析的方法进行。为此，用下面的方法对Q（Y）进行估计。

定义

于是，有

因此可以用统计试验的方法估计Q（Y）。首先产生概率密度函数为p（y）的随机数y，然后计算DY（y），通过多次试验估计DY（y）的平均值可作为Q（Y）的估计值。下面考察DY（y）的方差。

因为虚警概率一般很小，即Q（Y）＜＜1。因此P（Y）≈1，所以DY（y）的方差可以近似为

N 次试验估计DY（y）的平均值为

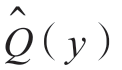的统计平均值和方差分别为

可见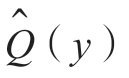的方差随N 的增加而减小。为使估计值具有实际意义，一般要求估值的标准差（均方差）远小于均值，即

即要求

例如Q（Y）=106，则要求N ＜＜106。因为Q（Y）=10-6 意味着DY（y）=1 平均在106 次试验中才有可能出现一次，所以只有N ＜＜106 时上述估值才有意义。由此可见对小概率事件的模拟试验，要达到一定的精度必须进行很多次的试验，这给实际应用带来了一定的困难。

上述情况出现的原因是所要模拟的事件在所进行的试验中出现的概率很小，相当于用蒙特卡洛模拟计算示意图2-26中黑色部分的面积。由于所要计算的面积太小，因而很难保证精度。若能改变p（y）曲线，使Q（Y）所包含的面积增加（图2-26 中阴影部分的面积），则比较容易计算。

图2-26　蒙特卡洛模拟计算Q（ Y ）示意图

重要采样技术是雷达系统中估计虚警概率以及通信系统中估计错误概率等小概率事件的计算机仿真实验中常用的一种方差修正方法，其基本思想是修改原来的随机变量，使所关心的小概率事件出现的概率变大。对于上面的问题，应当使对Q（Y）贡献较大的（即曲线尾部）y 多出现一些。为此，可以改变y，使其概率密度函数变为pm（y）。若对分布改变的随机变量用同样的门限y 进行上述处理，则得到的结果不再是Q（Y）。为了使得最后得到的结果仍然是Q（Y），应对上述的修改进行补偿。方法是在DY（y）后乘上一个加权系数w（y），处理过程如图2-27 所示。

图2-27　重要采样原理框图

从而使E[zm]= Q（Y），即

为使上式成立，应有

采用重要采样技术提高蒙特卡洛模拟效率的具体做法是：首先对所要模拟的随机变量ッ的概率密度函数p（y）进行修改，结果记为pm（y），对应的随机变量为ym。修改p（y）的目的是使感兴趣的事件（这里是p（y）曲线的尾部）出现的概率增加，从而可以用较少次数的试验取得较高的精度。为了使修改之后的随机变量均值的估计值仍为所期望的值，在计算估值前用w（y）对其进行补偿，即按下式计算Q（Y）的估值。

其中，DY（yi）为概率密度函数修改之后的随机变量ym 与门限Y 比较之后的结果。

（二）重要采样实例

1.指数分布情况

如何应用重要采样原理以较少的试验次数获得精度较高的Q（Y）的估计值？下面以指数分布随机变量为例，对该问题进行展开。

设

易得

下面用蒙特卡洛模拟通过重要采样技术计算Q（Y）。为了减少试验次数，改变p（y），即加大λ 值。修改后的概率密度函数为

于是(www.daowen.com)

令

则

所以

若进行N 次独立试验并计算

则

所以

假设λm ＜＜λ，于是上式可近似为

下面讨论如何确定λm 对于给定的N 使上式达到最小。为此，上式对λm 求导数，并令结果等于零，即

解出

在最小值处

若取Q（Y）=10-6，则根据计算可得，Y=13.8λ，因而λ_m=13.8λ，可得

若直接进行蒙特卡洛模拟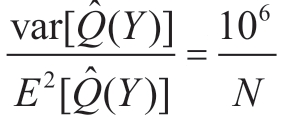，。可见对于相同的试验次数，采用重要采样技术得到的Q（Y）的精度大大提高。本例中Q（Y）有解析表达式，可以进行计算，实际当中并不需要利用蒙特卡洛模拟来估计。下面的例子则由于Q（Y）没有解析表达式，蒙特卡洛模拟是一种代替数值计算的实用的方法。

2.高斯分布情况

设x 为零均值，方差为σ2 的高斯分布随机变量，即

利用重要采样原理计算。修改p（x），将其方差改为，即

有

于是，有

σm 的选择应使上式达到最小。对于给定的Y，可用数值方法求上式最小值对应的σm。Q（Y）不同，Y 也就不同，求出的最佳σm 也不同。例如，若Q（Y）=10-6，或Y = 4.7σ，则σm = 4.78σ。但在4.0 ＜ σm/σ ＜5.5 范围内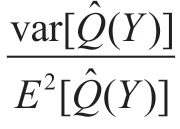，的值变化不大。因而，在一定范围内可选σm ≈ Y。

3.试验结果

图2-28（a）和图2-28（b）分别给出了利用重要采样计算λ=1 的指数分布Q（Y）的1 000 次和10 000 次蒙特卡洛试验结果。图中实线表示蒙特卡洛试验结果，虚线为理论计算结果。根据前面分析，对于参数λ=1 的指数分布，若Q（Y）=10-6，λm 的最佳值为13.8。但试验结果λm 在很大范围内（5 ～50），都能取得满意的结果。

图2-28　利用重要采样计算指数分布Q（Y）的模拟结果（实线）与理论计算结果（虚线）对比

（a）N=1 000；（b）N=10 000

图2-29（a）和图2-29（b）分别给出利用重要采样计算标准正态分布（均值为零、方差为1）Q（Y）的1 000 次和10 000 次蒙特卡洛试验结果。图中实线表示蒙特卡洛试验结果，虚线为理论计算结果。根据前面分析，方差等于1 的正态分布，在Q（Y）=10-6 附近，λm 的最佳值为4.78，实验表明λm 在2 ～8 范围内取值，蒙特卡洛试验结果与理论值都很接近。

试验结果表明，对于Q（Y）=10-6，利用重要采样技术计算指数分布的Q（Y），蒙特卡洛试验次数N=1 000 便可达到很高的精度。在Q（Y）=10-6 附近，利用重要采样技术计算正态分布的Q（Y），蒙特卡洛试验次数N=10 000 便可达到很高的精度。若直接进行蒙特卡洛试验，则两者的试验次数至少都要大于107。

图2-29　利用重要采样计算正态分布Q（Y）的模拟结果（实线）与理论计算结果（虚线）对比

（a）N=1 000；（b）N=10 000