（一）均匀分布随机数的产生

产生均匀分布随机数的方法有多种，在这里主要介绍乘同余法。乘同余法用下面的迭代公式产生均匀分布随机数

其中，λ 为乘因子；M 是模数；mod 表示模除。给定一个初始值x0 后，便可按上式递推x1，x2，…，xn。因为xi 的取值为0 ～M-1 之间的整数，所以最多有M个不同的值，即序列{xi}是周期性重复的，重复周期L ≤ M。但若L 足够大，在一次试验时间内，可以将{xi}当作随机数。显然，xn 服从均匀分布。只要λ、x0 和M 选得合适，就可以用这种方法产生满足要求的随机数。例如，对于32 位的long integer 类型，可以选择xn=65 539·xn-1（mod231），因65 539=216+3，所以该乘法可以用移位和加法实现。xn 在[0，M]上均匀分布，令yn=xn/M 在[0，1]上均匀分布。均匀分布随机数是产生任意分布随机数的基础。有多种方法由均匀分布随机数来产生其他分布的随机数。

图2-24　估计量的均值偏差及方差与SNR 的关系

（二）任意分布随机数的产生

1.反函数法

若随机变量η 的连续分布函数为F（x），而ξ 是在[0，1]上均匀分布的随机数，其概率密度函数记为g（x），分布函数记为G（x），如图2-25 所示。则

图2-25　均匀分布随机变量的概率密度函数和分布函数

证明：

第一步根据公式得到。第二步是根据任意随机变量的分布函数为单调不减函数，所以用F（x）作用在上式右端括号内的不等式两端该不等式仍成立。第三步是根据分布函数的定义得到的。最后一步利用了均匀分布随机数的分布函数的特点（图2-25）。表明，由均匀分布随机数ξ 产生的随机数η 的分布函数为F（x）。

也可以写成

若进一步假设具有概率密度函数（），则可以写成

因此，利用在[0，1]上均匀分布的随机数ξ，通过解上述方程便可得到概率密度函数为f（x）的随机数。这种方法要求F（x）的反函数存在。

2.坐标变换法

（1）正态分布随机数的产生(www.daowen.com)

设ξ1 和ξ2 是两个相互独立在[0，1]上均匀的随机数，进行如下变换

则η1 和η_2 是两个相互独立的N（0，1）正态分布随机数。

证明：ξ1 和ξ2 的联合概率密度函数为

所以η1 和η2 的联合概率密度函数为

其中，J 为雅可比行列式。

由上式可解出

从而可得雅可比行列式的值为

故

即f（η1 和η2）为两个相互独立的N（0，1）分布的乘积。所以η1 和η2 为相互独立的服从N（0，1）分布的随机数。有了N（0，1）分布的随机数很容易产生N（m，σ2）分布的随机数。

（2）瑞利分布随机数的产生瑞利分布随机数的概率密度函数为

因为瑞利分布是二维正态分布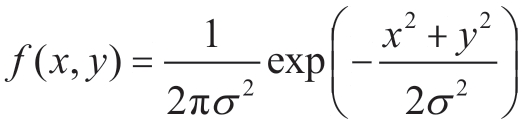的随机数x 和y 的幅度images/P56_294934.jpg的分布，所以瑞利分布随机数可以这样产生：

① 产生两个相互独立的正态分布N（0，σ2）随机数（x 和y）。

② 计算，则「即为参数为ぴ的瑞利分布随机数。