当不能用数值计算方法确定随机变量超过某一给定值的概率时，可借助蒙特卡洛计算机模拟方法。在检测问题中，常需要计算一个随机变量或统计量T 超过某门限γ 的概率，即Pr{T ＞γ}。

例如，某数据集{ x[0]，x[1]，…，x[N-1]}，其中x[n]～N（0，σ2），且x[n]是独立同分布的，希望计算

由于可证明

因而

式中，Q（x）是标准正态变量超过x 的概率。

然而，假定不能使用解析的方法，也不能用数值计算的方法计算概率，可以按如下的方法使用计算机模拟来确定Pr（T ＞γ）。

数据产生：

（1）产生N 个独立的N（0，σ2）随机变量。在MATLAB 中，使用语句

产生随机变量x[n]的实现组成的N×1 列矢量，其中，var 是方差σ2。(www.daowen.com)

（2）对随机变量的实现计算

（3）重复过程M 次，以便产生T 的M 个实现，或者（T1，T2，…，TM}。概率计算：

（1）对Ti 超过γ 的次数统计，称为Mr。

（2）用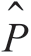 = Mr / M 来估计概率Pr（T ＞γ）。

注意，这个概率实际上是一个估计概率。M 的选择（也就是实现数）将影响结果，以至于Mr 应该逐步增大，直到计算的概率出现收敛。如果真实概率较小，那么Mr 可能相当大。例如，如果Pr（T ＞γ）= 10-6，那么M =106 个实现中将只有一次超过门限，在这种情况下，Mr 必须远大于106 才能保证精确的估计概率。如果希望对于100（1-α）%的置信水平，相对误差的绝对值为

那么，选择的应该满足

式中，P 是被估计的概率。为了使用蒙特卡洛实现{T1，T2，…，TM}来确定Pr（T＞γ），对实现数提出一定的要求是合理的，实现{T1，T2，…，TM}是从独立的随机变量中得到的。随机变量了，一般不必是高斯的，只要是独立同分布的（IID）。例如，如果希望确定Pr（T ＞1），这个概率P 为0.16，要求对于95%的置信水平，相对误差的绝对值为∈= 0.01（1%），那么

当这种方法不可行时，可以采用重要采样（Importance Sampling）来减少计算量。