（一）理想实白噪声过程的希尔伯特变换

理想实白噪声过程X（t）的功率谱密度为GX（ω）= n0/2，自相关函数为GX（τ）=（n0/2）δ（t）。X（t）的希尔伯特变换记作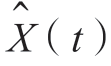，则根据希尔伯特变换的性质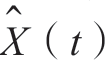，的自相关函数为的互相关函数为GXX（τ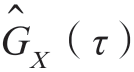）=。变换后得到的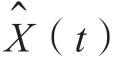仍为高斯白噪声，但X（t）与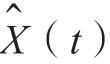只有在同一时刻不相关。

图2-21 所示为利用Matlab 中的hilbert（）函数对高斯白噪声进行离散希尔伯特变换，通过10 000 次蒙特卡洛试验得到的x（n）与其离散希尔伯特变换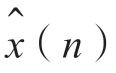的互相关函数的结果。

图2-21　白噪声序列与其离散希尔伯变换的互相关函数仿真结果

Z（t）是利用X（t）与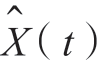构成的解析噪声，根据解析过程的性质，Z（t）的自相关函数为

图2-22　解析噪声过程的PSD

可知，Z（t）不是（复）白噪声。图2-22 是利用相关函数的DFT 得到的解析噪声Z（t）的功率谱密度GZ（k）的10 000 仿真平均的结果，DFT 点数N = 50。可见其PSD 并不是恒定的。(www.daowen.com)

（二）带限白噪声的希尔伯特变换

低通白噪声过程X（t）的功率谱密度可表示为

X（t）的自相关函数为

图2-23　窄带白噪声与其希尔伯特变换的互相关函数

用低通白噪声X（t）和其希尔伯特变换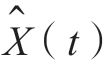构成的解析噪声过程Z（t）= X（t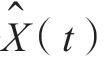）+的自相关函数为

综上，由高斯白噪声经过希尔伯特变换得到的解析噪声过程不是白噪声。