对于一个连续随机信号X（t），以Ts 为间隔进行等间隔的采样，可以得到一个随机序列，表示为

由于X（t）是随时间t 变化的随机变量，X（n）自然是随着n 变化的随机变量，称为时域离散随机信号（离散随机过程）。因整数n 代表等间隔的时间增量，随机序列也常称为时间序列。

X（n）的实现或样本函数记为x（n），X（n）和x（n）常记为Xn 和xn。

（一）随机序列的统计描述

1.概率密度函数

随机序列X（n）的一维概率分布函数和一维概率密度函数分别定义为

二维概率分布函数和二维概率密度函数分别定义为

依此类推，可以得到对应的N 维概率分布函数和N 维概率密度函数，即

概率密度函数具有如下主要特性。

（1）概率密度函数p（x）是非负的，即

（2）概率密度函数p（x）的全域积分等于1，即

（3）离散随机信号x 落在[a，b]区间的概率P（a ≤ x ≤ b），等于其概率密度函数p（x）在该区间的积分，即

2.离散随机信号的统计平均量

离散随机序列的数学期望

离散随机序列的均方值

离散随机序列的方差

离散随机序列的自相关函数与自协方差函数分别定义为

以上是从随机过程的角度进行的统计描述。对于一个固定的n，X（n）是一个随机变量，一个N 点有限长的随机序列可以构成一个N 维的随机向量，记为X = [X1，X2，…，XN]T。因此，可以从随机向量的角度研究随机序列。定义均值向量为

自相关矩阵为

协方差矩阵为

容易证明，协方差矩阵与自相关矩阵之间的关系为

对于一般随机序列，自相关矩阵与协方差矩阵具有以下两个性质：

（1）厄米特（Hermitian）对称性：

（2）半正定性：即对任意N 维非随机向量，f = [f1，f2，…，fN]T，总有，f H RX f ≥ 0，f H CX f ≥ 0。

注意：对于矩阵A，AT 是A 的转置，AH 则是A 的Hermitian 转置（共轭转置），对于实矩阵有AT = AH。

（二）平稳随机序列

与连续平稳随机过程概念相同，严格平稳随机序列，是指它的N 维概率分布函数或N 维概率密度函数与时间n 的起始位置无关，其统计特征不随时间的平移而发生变化。如果将随机序列在时间上平移k，其统计特征满足

同样，如果一个随机序列的均值和均方差不随n 改变，相关函数仅是时间差的函数，则将其称为广义（宽）平稳随机序列，简称为平稳随机序列。即对于平稳随机序列，有

对于两个各自平稳且联合平稳的随机序列，其互相关函数与互协方差函数分别为

显然，对于自相关函数和互相关函数，有（-m）。同样，如果CXY（m）=0，称两个随机序列互不相关；如果RXY（m）=0，称两个随机序列正交。

对由N 点有限长平稳随机序列构成的N 维随机向量X = [X1，X2，…，XN]T，其自相关矩阵式和协方差矩阵式除满足对称性与半正定性外，均为厄米特-托普利（Hermitian-Toeplitz）矩阵。自相关矩阵（协方差阵类似）可写为

该矩阵左上右下对角线上的元素均相同，此性质根据平稳随机序列的定义容易证明。这样只需要知道第一行或第一列元素的值，则整个矩阵便可唯一确定。对实平稳随机序列，对应实矩阵，就是常用的托普利兹矩阵形式。托普利兹矩阵在数字信号处理的快速算法中特别有用，对该形式矩阵的求逆、分解等各种运算的快速算法研究也是一个专门的方向。设x（n）是平稳随机序列X（n）的一个样本序列，其时间平均定义为

时间自相关函数为

如果平稳随机序列X（n）满足(www.daowen.com)

则称此随机序列具有各态历经性。与连续随机过程一样，对于各态历经的随机序列，我们可以直接用它的任一个样本函数的时间平均来代替对整个随机序列统计平均的研究，从而给许多实际问题的解决带来了很大方便。

平稳随机序列的功率谱密度定义为其自相关函数的傅里叶变换，即

其逆变换为

上述两式就是平稳随机序列的维纳-辛钦定理。对于实平稳序列，其功率谱具有如下性质：

1.功率谱是ω 的偶函数，即SX（ω）= SX（-ω）。

2.功率谱是实的非负函数，即SX（ω）≥ 0。

（三）随机信号的采样定理

我们已经学习了确定性信号的采样定理，为了不丢失信息，换句话说，能够由时域离散信号准确地恢复原模拟信号，要求采样频率必须大于等于信号最高频率的两倍以上。对于平稳随机信号的采样也有类似的结论。

对于平稳随机信号，如果其功率谱严格限制在某一有限频带内，该随机信号称为带限随机信号。如果平稳随机信号X（t）的功率谱SX（ω）满足

则称为低通带限随机信号。其中，ωc 表示功率谱的最高截止频率。

设以采样间隔乃对平稳随机信号X（t）进行采样，采样后随机序列为X（n），当采样频率满足时，采样插值公式为

可以证明，在均方意义上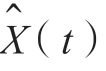，等于X（t），即。也可以表示为对X（t）的采样展开形式，即

其中，lim 用于表示在均方意义下的收敛。

上式表明，一个平稳连续随机过程X（t）可以用一族确定的正交函数基sinωc（tnTs）/ωc（t- nTs）的展开来表示，而基函数的系数就是该过程在固定间隔采样后的随机变量X（n）。但对于非平稳随机过程，上式并不成立。此外，由于自相关函数和功率谱是对所有样本统计平均计算的结果，所以，上式只在统计平均意义下成立。对于X（t）的某一个样本函数（实现）x（t），若其采样序列为x（n），则

并不总成立，因为确定信号x（t）的带宽完全可能大于采样频率。这是随机信号采样和确定信号采样理论在概念上的不同之处。

为了讨论X（t）与X（n）功率谱之间的关系，暂时记X（t）的功率谱为SXt（ω），自相关函数为RXt（τ），X（n）的功率谱为SXn（ω），自相关函数为RXn（m）。由于RXn（m）是RXt（τ）的采样结果，采样间隔也是Ts，自相关函数与功率谱是傅里叶变换对的关系，且均是确定性函数，所以，可以得到与确定性信号采样完全相同的结论，即

即时域离散化带来频域功率谱的周期化，且周期就是采样频率。

（四）时间序列信号模型

对于平稳随机序列，除了用自相关函数和功率谱进行研究外，还可以从时间序列分析的角度进行研究，即时间序列信号模型方法。基本思想是将所要研究的平稳随机序列看作一个由典型噪声序列u（n）激励一个线性系统而产生的输出。这种噪声源一般是自序列，信号模型如图2-2-8 所示。其中，H（z）是该线性稳定系统的系统函数。

图2-5　信号模型

假设信号模型用一个阶差分方程描述，即

根据系数取值的情况，将模型分为以下三种。

1.滑动平均模型（Moving Average，MA）

当上式中ai = 0（i = 1，2，…，p）时，该模型称为MA 模型。其模型差分方程和系统函数分别表示为

本式表明该模型只有零点，没有除原点以外的极点。因此，该模型也称为全零点模型。如果模型全部零点都在单位圆内部，则是一个最小相位系统，且模型是可逆的。

2.自回归模型（Autoregressive，AR）

模型差分方程和系统函数分别为

此式表明该模型只有极点，没有除原点以外的零点。因此，该模型也称为全极点模型。只是当全部极点都在单位圆内部时，模型才稳定。

3.自回归-滑动平均模型（ARMA）

当模型差分方程式中ai = 0（i = 1，2，…，p）和bi = 0（i = 1，2，…，q）均不全为零时，则模型称为ARMA 模型。所对应的系统函数为

若u（n）是均值为0、方差为σ2 的自序列，则由随机信号通过线性系统的理论可知，输出序列的功率谱为

AR 模型、MA 模型和ARMA 模型是功率谱估计中最主要的参数模型，也是现代谱估计理论的基础。其中，AR 模型的正则方程是一组线性方程，而MA 模型和ARMA 模型是非线性方程。由于AR 模型具有一系列好的性能，所以，该模型是一种研究最多并获得广泛应用的模型。