（一）连续随机过程的基本概念

如果所研究的对象具有随时间演变的随机现象，对其全过程进行一次观测得到的结果是时间t 的函数，但对其变化过程独立地重复进行多次观测，则所得到的结果仍是时间t 的函数，而且每次观测之前不能预知所得结果，这样的过程就是一个随机过程。

类似于随机变量的定义，可给出随机过程的定义：设E 是随机试验，它的样本空间S={ ζ }，若对于每个ζ ∈S，总有一个确知的时间函数x（t，ζ），t ∈T 与它相对应，这样对于所有的ζ ∈S，就可得到一族时间t 的函数，称为随机过程。通常为了简便，书写时省去符号ζ，而将随机过程记为X（t）。族中的每一个函数称为这个随机过程的样本函数。

对于一个特定的试验结果ζi，则x（t，ζi）是一个确知的时间函数，记为x1（t），x2（t），…，称为样本空间中的一族样本函数。对于一个特定的时间t，（ti，ζ）取决于ζ，是个随机变量，记为X1（t），X2（t），…。根据随机过程的定义，可以用如图2-1 所示的图形来描述一个连续的随机过程。

研究一族随机变量X1（t），X2（t），…的统计平均特性称为集平均，而研究某一样本函数的统计平均特性称为时间平均。

图2-1　连续随机过程的个样本函数图形

（二）连续随机信号的概率密度函数

连续随机信号x（t）在tk 时刻采样的样本为x（tk）=（xk；tk）（k=1，2，…，N），每个样本都是一个离散随机信号。对于任意N 和t1，t2，…，tN，样本x（tk）=（xk；tk）（k=1，2，…，N）构成N 维离散随机信号矢量（x；t）=（x1，x2，…，xN，t1，t2，…，tN）T，它的N 维联合概率密度函数

称为连续随机信号x（t）的N 维概率密度函数。

当N = 1 和任意tk；N = 2 和任意tj，tk，以及N ≥ 3 和任意t1，t2，…，tN 时，连续随机信号x（t）的1 维、2 维、…、N 维概率密度函数分别为

它们是x（t）全部统计特性的数学描述。

（三）随机过程的统计平均量

随机过程的概率密度函数描述需要很多信息，这些信息在实际中有时是很难全部得到的。然而，随机过程的许多主要特性可以用与它的概率密度函数有关的一阶和二阶统计平均量来表示，有的甚至完全由一阶和二阶统计平均量确定，如高斯随机过程。下面对随机过程的一阶和二阶统计量予以讨论。

将对随机变量数字特征的描述方法推广到随机过程，其区别在于随机变量的数字特征是确定的数值，而随机过程的数字特性是确定的时间函数。

1.随机过程的均值

随机过程的均值函数μx（t）在t 时刻的值表示随机过程在该时刻状态取值的理论平均值。如果X（t）是电压或电流，则μx（t）可以理解为在t 时刻的“直流分量”。

2.随机过程的均方值

如果X（t）是电压或电流，则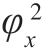（t）可以理解为t 时刻它在1Ω 电阻上消耗的“平均功率”。

3.随机过程的方差

式中，σx（t）称为随机过程的标准偏差。方差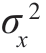（t）表示随机过程在t 时刻其取值偏离其均值μx（t）的离散程度。如果X（t）是电压或电流，则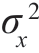（t）可以理解为t 时刻它在1Ω 电阻上消耗的“交流功率”。

容易证明

4.随机过程的自相关函数

随机过程的自相关函数RX（tj，tk），可以理解为随机过程的两个随机变量X（tj）与X（tk）之间含有均值时相关程度的度量。显然

5.随机过程的自协方差函数

随机过程的自协方差函数CX（tj，tk）表示随机过程的两个随机变量X（tj）与X（tk）之间的相关程度。它们的自相关系数定义为

容易证明

且有

6.随机过程的互相关函数

对于两个随机过程X（t）和Y（t），其互相关函数定义为

式中，p（xj，tj；yk，tk）是X（t）和Y（t）的二维混合概率密度函数。

7.随机过程的互协方差函数

随机过程X（t）和Y（t）的互协方差函数CXY（tj，tk）表示它们各自的随机变量X（tj）与Y（tk）之间的相关程度，实际上表示两个随机过程X（t）和Y（t）之间的相关程度。它们的互相关系数定义为

容易证明

（四）随机过程的平稳性和遍历性

1.严平稳过程

如果对于任意时刻τ，随机过程x（t）的n 维概率密度函数满足

即n 维概率密度函数不受时间起点的影响，则称x（t）是严平稳过程。

当n = 1 时，式（2-3-16）为

即平稳过程的一维概率密度函数与时间无关，通常记作p（x）。由此很容易推断平稳过程的均值和方差都与时间无关。平稳过程的二维概率密度函数与两个时刻t1 和t2 的绝对值无关，只与时间间隔τ = t1-t2 有关，即

平稳过程的自相关函数只与时间间隔有关，即

同理平稳过程的协方差函数也只与时间间隔有关。

判断随机过程是否为严平稳的，需要根据n 维概率密度函数是否与时间起点有关来进行，这在实际当中通常是很难做到的。而宽平稳的定义只用到随机过程的一、二阶矩。

2.广义平稳过程

若随机过程（）的均值和相关函数存在且满足：

（1）μx（t）

（2）RX（t，t+τ）=RX（t）

（3）E｛X2（t）｝＜∞

则称X（t）是宽平稳随机过程，又称为广义平稳过程。在没有特殊声明的情况下，实际应用中所说的平稳过程一般都指广义平稳过程。

若两个广义平稳随机过程X（t）和Y（t）的互相关函数满足RXY（t，t+τ）=RXY（t），则称X（t）和Y（t）是联合广义平稳过程。

3.非平稳的连续随机信号

既不满足严格平稳，也不满足广义平稳的连续随机信号，称为非平稳的连续随机信号。

4.各态历经随机过程

定义样本函数的时间均值为

其中，x（t）为随机过程X（t）的某一个样本函数；T 为观测区间。(www.daowen.com)

时间相关函数是时间平均的自相关函数，定义为

一般来说，不同样本函数的时间平均不一定相同，而其集平均是一定的，因此，一般随机过程的时间平均并不等于其集平均。

如果一个平稳随机过程，它的各种集平均都以概率1 等于其相应的各种时间平均，则称该平稳随机过程是“各态历经的”，或者说该过程是“遍历的”。

如果对于平稳随机过程X（t）的所有样本函数而言，有

以概率1 成立，则称此过程的均值具有各态历经性。

如果对于平稳过程X（t）的所有样本函数而言，有

以概率1 成立，则称此过程的自相关函数具有各态历经性。若仅当τ = 0 时，式（2-2-23）成立，则称X（t）的均方值具有各态历经性。

如果上述两式均以概率1 成立，则称平稳随机过程X（t）是宽各态历经过程。下面除非特别指出，提到的各态历经均指宽各态历经。

对两个随机过程X（t）和Y（t），如果它们各自都是各态历经的，并且时间互相关函数与统计互相关函数以概率1 相等，即

则称这两个随机过程是联合各态历经的。

对一般随机过程而言，时间平均将是一个随机变量；但对各态历经过程而言，由上述定义可知，时间平均得到的结果趋于一个非随机的确定量。这就表明各态历经过程各样本函数的时间平均实际可以认为是相同的。于是，随机过程的时间平均也就可以由样本函数的时间平均来表示。因此，对于这类随机过程，我们可以直接用它的任意一个样本函数的时间平均来代替对整个随机过程统计平均的研究。这也正是引入各态历经概念的重要目的。这些性质给许多实际问题的解决带来了很大方便。例如，测量接收机的噪声，用一般的方法，就需要在同一条件下对数量极多的相同接收机同时进行测量和记录，然后用统计方法计算出所需的数学期望、相关函数等数字特征。若利用随机过程的各态历经性，则只要用一部接收机，在环境条件不变的情况下，对其输出进行长时间的记录，然后用求时间平均的方法，即可求得数学期望和相关函数等数字特征。当然，由于实际中对随机过程的观察时间总是有限的，因而取时间平均时，只能用有限的时间代替无限的时间，会给结果带来一定误差，这也是统计估值理论要解决的基本问题。

随机过程X（t）=Y，Y 是方差不为零的随机变量。由于E{ X（t）}=而（X（t）） = Y。Y 是随机变量，E（Y）是常数，显然不满足各态历经性的条件，因此X（t）不是各态历经过程，随机过程X（t）= Y 的群本函数如图2-2 所示。

图2-2　随机过程X（t） = Y 的样本函数

图2-2 所示相当于有很多经过特殊处理的色子，每个色子都只能出现1 ～6个数字当中的某一个。如果同时掷这些色子，则出现1 ～6 当中每个数字的色子的个数几乎是一样的，但如果反复掷一枚色子则总是出现同一个数字。显然这个过程不具有各态历经性，即某一个样本函数不论多长时间都不会经历随机过程的全部状态。

长时间跟踪具有各态历经性的随机过程的一个样本函数会经历随机过程全部的状态空间。图2-3 和图2-4 分别表示很长时间观测两个随机过程记录的样本函数。则大概可以判断图2-3 代表的随机过程不具有各态历经性，图2-4 代表的随机过程有可能具有各态历经性。

图2-3　不具有各态历经性的随机过程的样本函数

图2-4　具有各态历经性的随机过程的样本函数

（五）连续随机信号的正交性、互不相关性和相互统计独立性

1.定义

（1）若连续随机信号的自相关函数满足

或平稳条件下满足

则称连续随机信号的两个样本X（tj）与X（tk）之间是正交的。

（2）若连续随机信号的自协方差函数满足

则称连续随机信号的两个样本X（tj）与X（tk）之间是互不相关的。

（3）若连续随机信号x（t）的N 维概率密度函数p（x；t）满足

则称连续随机信号的样本X（tj）与X（tk）之间是相互统计独立的。

2.关系

若随机过程X（t），其相互正交随机变量过程、互不相关随机变量过程和相互统计独立随机变量过程三者之间的关系有如下三个结论。

结论Ⅰ：如果μx（tj）= 0，μx（tk）= 0，则相互正交随机变量过程等价为互不相关随机变量过程。

结论Ⅱ：如果X（t）是一个相互统计独立随机变量过程，则它一定是一个互不相关随机变量过程。

结论Ⅲ：如果X（t）是一个互不相关随机变量过程，则它不一定是相互统计独立随机变量过程，除非其随机变量是服从联合高斯分布的。这一结论可推广到任意N 维的情况。这是高斯随机变量过程的又一重要特性，非常有用。

现在讨论两个随机过程X（t）和Y（t）之间的这些特性。设X（tj）是X（t）在tj 时刻的随机变量，Y（tk）是Y（t）在tk 时刻的随机变量。如果

对于任意的tj 和tk 时刻都成立，则称X（t）和Y（t）是相互正交的两个随机过程。如果

对于任意的tj 和tk 时刻都成立，则称X（t）和Y（t）是互不相关的两个随机过程，其等价条件为如果X（t）和Y（t）是联合平稳的随机过程，则当

时，X（t）和Y（t）是相互正交的平稳过程；而当

或

时，X（t）和Y（t）是互不相关的平稳过程。

如果随机过程X（t）和Y（t）对任意的N ≥ 1，M ≥ 1 和所有时刻tk（k = 1，2，…，N）与（k=1，2，…，M），其N + M 维联合概率密度函数都能够表示为

则称X（t）和Y（t）是相互统计独立的两个随机过程。

显然，若X（t）和Y（t）的均值之一或同时等于零，则相互正交的X（t）和Y（t）也是互不相关的随机过程。若X（t）和Y（t）是相互统计独立的两个随机过程，则它们一定是互不相关的；互不相关的两个随机过程X（t）和Y（t）不一定是相互统计独立的，除非它们服从联合高斯分布，互不相关的两个过程才是统计独立的。

（六）平稳连续随机信号的功率谱密度

1.功率谱密度的概念

平稳连续随机过程X（t）的能量是无限的，不满足傅里叶变换的条件，但其功率通常是有限的，从而引出X（t）的功率谱密度PX（ω），用来描述其功率在频域的分布特性。

2.自相关函数与功率谱密度之间的关系

根据维纳-辛钦定理，平稳连续随机过程X（t）的自相关函数PX（τ）与功率谱密度PX （ω）之间构成傅里叶变换对，即

3.功率谱密度的主要性质

（1）PX（ω）是非负函数，即

（2）PX（ω）是ω 的偶函数，即

（3）PX（ω）与X（t）的平均功率的关系如下

因为PX（0）= E [X2（t）]是平稳连续随机信号X（t）的平均功率，所以上式是由PX（ω）与X（t）平均功率的频域公式。

4.互相关函数与互功率谱密度的关系

设X（t）和Y（t）是各自平稳且联合平稳的连续随机信号，则其互相关函数PXY（τ）与互功率谱密度PXY（ω）之间构成傅里叶变换对，即