GPS采用空间测距交会原理进行定位。如图8.1（b）所示，为了测定地面某点P在WGS-84坐标系中的三维坐标（xP，yP，zP），将GPS接收机安置在P点，通过接收卫星发射的测距码信号，在接收机时钟的控制下，可以解出测距码从卫星传播到接收机的时间Δt，乘以光速c并加上卫星时钟与接收机时钟不同步改正，就可以计算出卫星至接收机的空间距离ρ˜。

式（8.1）中，vt为卫星钟差，vT为接收机钟差。与EDM使用双程测距的方式不同，GPS使用单程测距方式，即接收机接收到的测距信号不再返回卫星，而是在接收机中直接解算传播时间Δt并计算出卫星至接收机的距离，这就要求卫星和接收机的时钟应严格同步，卫星在严格同步的时钟控制下发射测距信号。事实上，卫星钟与接收机钟不可能严格同步，这就会产生钟误差，两个时钟不同步对测距结果的影响为c（vT-vt）。卫星广播星历中包含有卫星钟差vt，它是已知的，而接收机钟差vT是未知数，需要通过观测方程解算。

式（8.1）中的距离ρ˜没有顾及大气电离层和对流层折射误差的影响，它不是卫星至接收机的真实几何距离，通常称其为伪距。

在测距时刻ti，接收机通过接收卫星Si的广播星历可以解算出Si在WGS-84坐标系中的三维坐标（xi，yi，zi），则Si卫星与P点的几何距离为

(www.daowen.com)

由此得伪距观测方程为

式（8.3）有xP，yP，zP，vT 4个未知数，为解算这4个未知数，应同时锁定4颗卫星进行观测。如图8.1（b）所示，对A，B，C，D这4颗卫星进行观测的伪距方程为

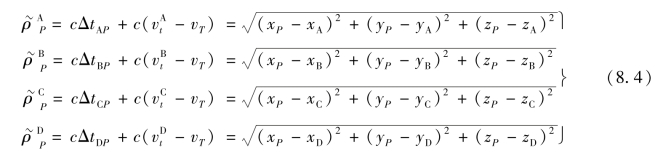
解式（8.4）即可计算出P点的坐标（xP，yP，zP）。