对某量进行不等精度独立观测，得观测值l1，l2，…，ln，其中误差分别为m1，m2，…，mn，权分别为W1，W2，…，Wn，则观测值的加权平均值为

将式（6.26）化为

应用误差传播定律得

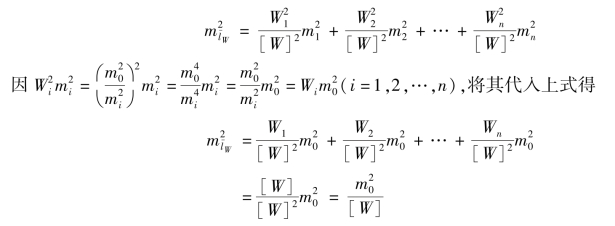
等式两边开根号得

下一节将证明：不等精度独立观测量的加权平均值的中误差最小。

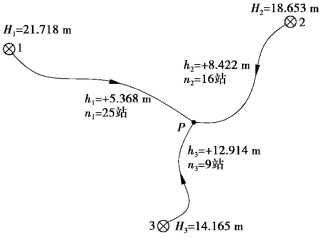
【例6.4】　如图6.4所示，1，2，3点为已知高等级水准点，其高程值的误差很小，可以忽略不计。为求P点的高程，使用DS3水准仪独立观测三段水准路线的高差，每段高差的观测值及其测站数标于图中，试求P点高程的最可靠值及其中误差。

【解】　因为都是使用DS3水准仪观测，可以认为其每站高差观测中误差m站相等。

由式（6.17）求得高差观测值h1，h2，h3的中误差分别为

取m0=m站，则h1，h2，h3的权分别为W1=1/n1，W2=1/n2，W3=1/n3。

由1，2，3点的高程值和3个高差观测值h1，h2，h3，分别计算出P点的高程值为

(www.daowen.com)

图6.4　某水准路线图

HP1=H1+h1=21.718 m+5.368 m=27.086 m

HP2=H2+h2=18.653 m+8.422 m=27.075 m

HP3=H3+h3=14.165 m+12.914 m=27.079 m

因为3个已知水准点的高程误差很小，可以忽略不计，所以前面求出的3个高差观测值的中误差m1，m2，m3就等于使用该高差观测值计算出的P点高程值HP1，HP2，HP3的中误差。

P点高程的加权平均值为

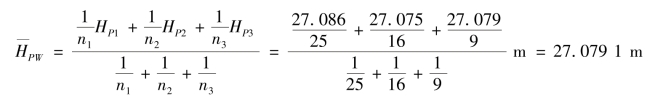
P点高程加权平均值的中误差为

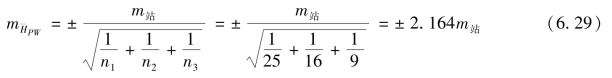
下面验证P点高程算术平均值的中误差P点高程的算术平均值为

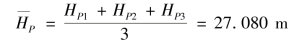
根据误差传播定律，求得P点高程算术平均值的中误差为

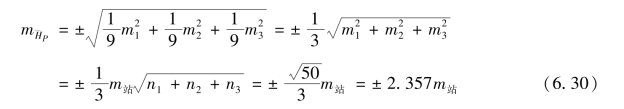
比较式（6.29）与式（6.30）的结果可知，对于不等精度独立观测，加权平均值比算术平均值更合理。